算額（その196） - 算額あれこれ

長野県下高井郡木島平村穂高一川谷大元神社文化8年(1811)
長野県飯山市下木島鳥出神社天保14年(1843)

中村信弥「改訂増補長野県の算額」県内の算額(P.91, 165)
http://www.wasan.jp/zoho/zoho.html
キーワード：円7個
#Julia #SymPy #算額 #和算 #数学

問1 2つの大円が交わっている部分に中円，それ以外の部分に小円が入っている。大円，中円の径が与えられたとき，小円の径を求めよ。

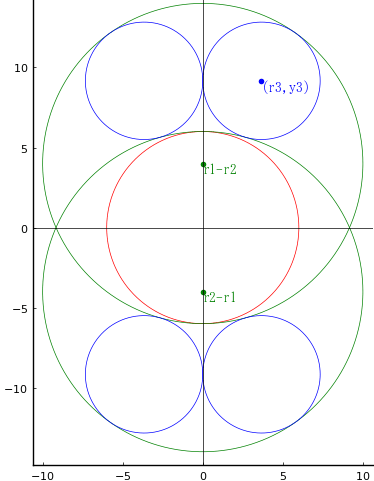
大円，中円，小円の半径を \(r_1,\ r_2,\ r_3\) とおく。
小円の中心の \(y\) 座標を \(y_3\) とおく。
以下の連立方程式を \(r_3,\ y_3\) について解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms r1::positive, r2::positive, r3::positive, y3::positive;

eq1 = r3^2 + (r1 - r2 + y3)^2 - (r1 + r3)^2 |> expand
eq2 = r3^2 + (r2 - r1 + y3)^2 - (r1 - r3)^2 |> expand
solve([eq1, eq2], (r3, y3))[1]

(sqrt(r2)*(r1 - r2)*sqrt(2*r1 - r2)/r1, sqrt(r2)*sqrt(2*r1 - r2))

式を変形して，小円の径は「（1 - 中円の径/大円の径）× 平方根(2×大円の径×中円の径 - 中円の径の二乗）」である。当然であるが，文中の「径」は「直径」と読み替えても「半径」と読み替えてもよい。

中円の径が大円の径に比して小さいと，「小円が中円より大きい」ということになる（その限界値を求めるのも一興である）。

\(r_1 = 10;\ r_2 = 4.56310987307924\)
\(r_3 = 4.5631098730792345;\ y_3 = 8.392867552141613\)

描画関数プログラムのソースを見る

function draw(r1, r2, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r3, y3) = (sqrt(r2)*(r1 - r2)*sqrt(2*r1 - r2)/r1, sqrt(r2)*sqrt(2*r1 - r2))
plot()
circle(0, 0, r2)
circle22(0, r1 - r2, r1, :green)
circle4(r3, y3, r3, :blue)
if more
point(0, r1 - r2, "r1-r2")
point(0, r2 - r1, "r2-r1")
point(r3, y3, "(r3,y3)", :blue)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
end
end;