算額（その179） - 算額あれこれ

長野県上田市別所温泉北向観音堂安永7年(1778)

中村信弥「改訂増補長野県の算額」(P.29)
http://www.wasan.jp/zoho/zoho.html
キーワード：累円，外円
#Julia #SymPy #算額 #和算 #数学

大円の中に天円 2 個，地円 2 個，人円 4 個を容れる。大円の径は 216 寸である。天, 地, 人, 甲, 乙, 丙, 丁, 戊, 己, 庚, 辛, 壬, 癸, 乾, 兌, 離, 震, 巽, 坎, 艮, 坤の各円の径を求めよ。

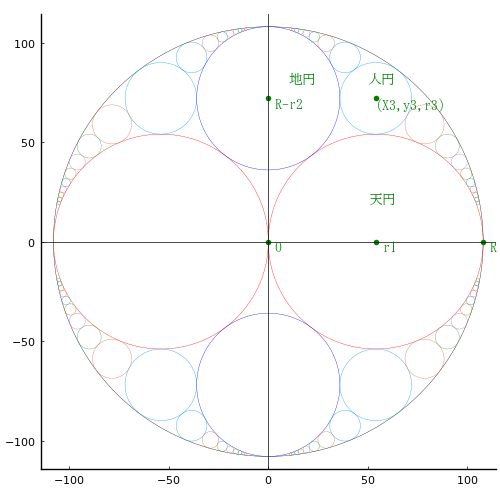
大，天，地，人円の半径と中心座標を \( (R,\ 0,\ 0),\ (r_1,\ r_1,\ 0),\ (r_2,\ 0,\ R - r_2),\ (r_3,\ x_3,\ y_3)\) とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms R::positive, r1::positive, r2::positive,
r3::positive, x3::positive, y3::positive,
r4::positive, x4::positive, y4::positive,
r5::positive, x5::positive, y5::positive,
r6::positive, x6::positive, y6::positive

eq5 = (x4 - x3)^2 + (y3 - y4)^2 - (r3 + r4)^2 # 円と次の円が外接する
eq6 = x4^2 + y4^2 - (R - r4)^2 # 次の円が外円に内接する
eq7 = (x4 - r1)^2 + y4^2 - (r1 + r4)^2 # 天円と次の円が外接する

eq8 = (x5 - x4)^2 + (y4 - y5)^2 - (r4 + r5)^2
eq9 = x5^2 + y5^2 - (R - r5)^2
eq10 = (x5 - r1)^2 + y5^2 - (r1 + r5)^2

eq11 = (x6 - x5)^2 + (y5 - y6)^2 - (r5 + r6)^2
eq12 = x6^2 + y6^2 - (R - r6)^2
eq13 = (x6 - r1)^2 + y6^2 - (r1 + r6)^2;

eq1 ~ eq4 を解いて \(r_2,\ r_3,\ x_3,\ y_3\) を得る。

res = solve([eq1, eq2, eq3, eq4], (r2, r3, x3, y3))[1]

(36, 18, 54, 72)

eq1 ~ eq13 を解くと \(r_2,\ r_3,\ x_3,\ y_3,\ r_4,\ x_4,\ y_4,\ r_5,\ x_5,\ y_5,\ r_6,\ x_6,\ y_6\) が得られる（1組目が適解）。

res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9, eq10,
eq11, eq12, eq13],
(r2, r3, x3, y3, r4, x4, y4, r5, x5, y5, r6, x6, y6))

3-element Vector{NTuple{13, Sym}}:
(36, 18, 54, 72, 108/11, 864/11, 648/11, 6, 90, 48, 4, 96, 40)
(36, 18, 54, 72, 108/11, 864/11, 648/11, 6, 90, 48, 108/11, 864/11, 648/11)
(36, 18, 54, 72, 108/11, 864/11, 648/11, 18, 54, 72, 108/11, 864/11, 648/11)

eq5, eq6, eq7 と eq8, eq9, eq10 を見れば，3つの連立方程式は漸化式になっている。そこで，以下の 3 連立方程式を \(r_i,\ x_i,\ y_i\) について，現在の円から次の円の半径，と中心座標を求める関数を定義する。

@syms ri, xi, yi, rip1, xip1, yip1
eq01 = (xip1 - xi)^2 + (yi - yip1)^2 - (ri + rip1)^2
eq02 = xip1^2 + yip1^2 - (R - rip1)^2
eq03 = (xip1 - r1)^2 + yip1^2 - (r1 + rip1)^2
res0 = solve([eq01, eq02, eq03], (rip1, xip1, yip1))

以下がその関数である。現在注目している円の半径，中心座標から，次の円の半径，中心座標を求める。

nextcircle(ri, xi, yi) = return ( (-ri^3 + 3*ri^2*xi - 108*ri^2 + ri*xi^2 - 216*ri*xi + ri*yi^2 + 11664*ri - 3*xi^3 + 756*xi^2 - 3*xi*yi^2 - 58320*xi + 540*yi^2 - 2*sqrt(2)*yi*sqrt(-ri^4 - 108*ri^3 + 2*ri^2*xi^2 - 108*ri^2*xi + 2*ri^2*yi^2 + 11664*ri^2 + 108*ri*xi^2 - 23328*ri*xi + 108*ri*yi^2 + 1259712*ri - xi^4 + 108*xi^3 - 2*xi^2*yi^2 + 11664*xi^2 + 108*xi*yi^2 - 1259712*xi - yi^4 + 11664*yi^2) + 1259712)/(2*(ri^2 - 6*ri*xi + 216*ri + 9*xi^2 - 648*xi + 8*yi^2 + 11664)), 3*(ri^3 - 3*ri^2*xi + 180*ri^2 - ri*xi^2 - 216*ri*xi - ri*yi^2 + 3888*ri + 3*xi^3 - 108*xi^2 + 3*xi*yi^2 + 11664*xi + 36*yi^2 + 2*sqrt(2)*yi*sqrt(-ri^4 - 108*ri^3 + 2*ri^2*xi^2 - 108*ri^2*xi + 2*ri^2*yi^2 + 11664*ri^2 + 108*ri*xi^2 - 23328*ri*xi + 108*ri*yi^2 + 1259712*ri - xi^4 + 108*xi^3 - 2*xi^2*yi^2 + 11664*xi^2 + 108*xi*yi^2 - 1259712*xi - yi^4 + 11664*yi^2) - 419904)/(2*(ri^2 - 6*ri*xi + 216*ri + 9*xi^2 - 648*xi + 8*yi^2 + 11664)), -4*yi*(ri^2 + 54*ri - xi^2 + 54*xi - yi^2 - 5832)/(ri^2 - 6*ri*xi + 216*ri + 9*xi^2 - 648*xi + 8*yi^2 + 11664) + sqrt(2)*sqrt(-(ri^2 - 108*ri - xi^2 + 108*xi - yi^2)*(ri^2 + 216*ri - xi^2 - yi^2 + 11664))*(ri - 3*xi + 108)/(ri^2 - 6*ri*xi + 216*ri + 9*xi^2 - 648*xi + 8*yi^2 + 11664));

人円を初期値として，甲，乙，丙...と求める。ここで，\(R\) を外円の半径 108 として順次求められる円の半径 \(r\) で割ったもの \(R/r\) が整数で，規則があることがわかる。すなわち，外円の半径と \(i\) 番目の円の半径の比は \(i^2 + 2i + 3\) である。

R = 108
(r, x, y) = (18, 54, 72)
@printf("i = 1; r = %g; R/r = %g\n", r, R/r)
for i = 2:10
(r, x, y) = nextcircle(r, x, y)
println("i = %d; r = %g; R/r = %g, %g\n", i, r, round(Int, R/r), i^2+2i+3)
end

i = 1; r = 18; R/r = 6.0
i = 2; r = 9.818181818181818; R/r = 11, 11
i = 3; r = 5.999999999999991; R/r = 18, 18
i = 4; r = 4.0; R/r = 27, 27
i = 5; r = 2.8421052631578947; R/r = 38, 38
i = 6; r = 2.117647058823516; R/r = 51, 51
i = 7; r = 1.6363636363636425; R/r = 66, 66
i = 8; r = 1.3012048192770946; R/r = 83, 83
i = 9; r = 1.058823529411749; R/r = 102, 102
i = 10; r = 0.8780487804877857; R/r = 123, 123

人円から始めて，乾，兌，離，震，巽，坎，艮，坤についても同様に行う。

using SymPy
@syms R, r1, r2, r3, x3, y3, r4, x4, y4

R = 216 // 2
r1 = R // 2
eq1 = r1^2 + (R - r2)^2 - (r1 + r2)^2 # 天円と地円が外接する
eq2 = (r1 - x3)^2 + y3^2 - (r1 + r3)^2 # 天円と人円が外接する
eq3 = x3^2 + (R - r2 - y3)^2 - (r2 + r3)^2 # 地円と人円が外接する
eq4 = x3^2 + y3^2 - (R - r3)^2; # 人円が外円に内接する
eq5 = (x3 - x4)^2 + (y4 - y3)^2 - (r3 + r4)^2 # 円と次の円が外接する
eq6 = x4^2 + y4^2 - (R - r4)^2 # 次の円が外円に内接する
eq7 = x4^2 + (y4 - R + r2)^2 - (r2 + r4)^2 # 地円と次の円が外接する

res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7], (r2, r3, x3, y3, r4, x4, y4))

4-element Vector{NTuple{7, Sym}}:
(36, 18, 54, 72, 54/7, 270/7, 648/7)
(36, 18, 54, 72, 54, 54, 0)
(36, 54, -54, 0, 18, -54, 72)
(36, 54, -54, 0, 54, 54, 0)

@syms r3, x3, y3, r4, x4, x5
r2 = 36
eq5 = (x3 - x4)^2 + (y4 - y3)^2 - (r3 + r4)^2 # 円と次の円が外接する
eq6 = x4^2 + y4^2 - (R - r4)^2 # 次の円が外円に内接する
eq7 = x4^2 + (y4 - R + r2)^2 - (r2 + r4)^2 # 地円と次の円が外接する
solve([eq5, eq6, eq7], (r4, x4, y4))

nextcircle2(r3, x3, y3) = return ( (-r3^3 + 2*r3^2*y3 - 108*r3^2 + r3*x3^2 + r3*y3^2 - 216*r3*y3 + 11664*r3 - 2*x3^2*y3 + 324*x3^2 - sqrt(3)*x3*sqrt(-r3^4 - 144*r3^3 + 2*r3^2*x3^2 + 2*r3^2*y3^2 - 144*r3^2*y3 + 7776*r3^2 + 144*r3*x3^2 + 144*r3*y3^2 - 31104*r3*y3 + 1679616*r3 - x3^4 - 2*x3^2*y3^2 + 144*x3^2*y3 + 7776*x3^2 - y3^4 + 144*y3^3 + 7776*y3^2 - 1679616*y3 + 45349632) - 2*y3^3 + 540*y3^2 - 46656*y3 + 1259712)/(2*(r3^2 - 4*r3*y3 + 216*r3 + 3*x3^2 + 4*y3^2 - 432*y3 + 11664)), (-3*r3^2*x3 - 216*r3*x3 + sqrt(3)*r3*sqrt(-r3^4 - 144*r3^3 + 2*r3^2*x3^2 + 2*r3^2*y3^2 - 144*r3^2*y3 + 7776*r3^2 + 144*r3*x3^2 + 144*r3*y3^2 - 31104*r3*y3 + 1679616*r3 - x3^4 - 2*x3^2*y3^2 + 144*x3^2*y3 + 7776*x3^2 - y3^4 + 144*y3^3 + 7776*y3^2 - 1679616*y3 + 45349632) + 3*x3^3 + 3*x3*y3^2 - 216*x3*y3 + 11664*x3 - 2*sqrt(3)*y3*sqrt(-r3^4 - 144*r3^3 + 2*r3^2*x3^2 + 2*r3^2*y3^2 - 144*r3^2*y3 + 7776*r3^2 + 144*r3*x3^2 + 144*r3*y3^2 - 31104*r3*y3 + 1679616*r3 - x3^4 - 2*x3^2*y3^2 + 144*x3^2*y3 + 7776*x3^2 - y3^4 + 144*y3^3 + 7776*y3^2 - 1679616*y3 + 45349632) + 108*sqrt(3)*sqrt(-r3^4 - 144*r3^3 + 2*r3^2*x3^2 + 2*r3^2*y3^2 - 144*r3^2*y3 + 7776*r3^2 + 144*r3*x3^2 + 144*r3*y3^2 - 31104*r3*y3 + 1679616*r3 - x3^4 - 2*x3^2*y3^2 + 144*x3^2*y3 + 7776*x3^2 - y3^4 + 144*y3^3 + 7776*y3^2 - 1679616*y3 + 45349632))/(2*(r3^2 - 4*r3*y3 + 216*r3 + 3*x3^2 + 4*y3^2 - 432*y3 + 11664)), sqrt(3)*x3*sqrt(-(-r3^2 - 216*r3 + x3^2 + y3^2 - 11664)*(-r3^2 + 72*r3 + x3^2 + y3^2 - 144*y3 + 3888))/(r3^2 - 4*r3*y3 + 216*r3 + 3*x3^2 + 4*y3^2 - 432*y3 + 11664) + (r3^3 - 2*r3^2*y3 + 216*r3^2 - r3*x3^2 - r3*y3^2 - 216*r3*y3 + 11664*r3 + 2*x3^2*y3 + 2*y3^3 - 108*y3^2)/(r3^2 - 4*r3*y3 + 216*r3 + 3*x3^2 + 4*y3^2 - 432*y3 + 11664));

R = 108
r2 = 36
(r, x, y) = (54/7, 270/7, 648/7)
for i = 1:10
println("%d, r = %g, x = %g, y = %g, %g, %g\n"), i, r, x, y, R/r, R/(2i^2 + 6i + 6))
(r, x, y) = nextcircle2(r, x, y)
end

1, r = 7.714285714285714, x = 38.57142857142857, y = 92.57142857142857, 14.0, 7.714285714285714
2, r = 4.153846153846184, x = 29.076923076923112, y = 99.69230769230774, 25.999999999999808, 4.153846153846154
3, r = 2.571428571428608, x = 23.142857142857242, y = 102.85714285714286, 41.9999999999994, 2.5714285714285716
4, r = 1.741935483871028, x = 19.16129032258083, y = 104.51612903225802, 61.99999999999786, 1.7419354838709677
5, r = 1.2558139534883404, x = 16.32558139534871, y = 105.48837209302322, 86.00000000000217, 1.255813953488372
6, r = 0.9473684210525465, x = 14.210526315789048, y = 106.10526315789478, 114.00000000001025, 0.9473684210526315
7, r = 0.7397260273971918, x = 12.575342465752794, y = 106.52054794520554, 146.0000000000135, 0.7397260273972602
8, r = 0.5934065934064815, x = 11.274725274724002, y = 106.81318681318686, 182.00000000003433, 0.5934065934065934
9, r = 0.48648648648640563, x = 10.216216216215297, y = 107.0270270270272, 222.0000000000369, 0.4864864864864865
10, r = 0.40601503759393454, x = 9.338345864660884, y = 107.18796992481218, 266.000000000033, 0.40601503759398494

\(R/r\) の数列は \(2i^2 + 6i + 6\) である。したがって，\(r_i = R/(2i^2 + 6i + 6)\) である。

描画関数プログラムのソースを見る

function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
R = 216 / 2
r1 = R / 2
(r2, r3, x3, y3) = (36, 18, 54, 72)
@printf("地円の半径 = %g, 人円の半径 = %g", r2, r3)
plot()
circle(0, 0, R, :black)
circle(r1, 0, r1, :red)
circle(-r1, 0, r1, :red)
circle(0, R - r2, r2, :blue)
circle(0, -R + r2, r2, :blue)
name1 = ["甲", "乙", "丙", "丁", "戊", "己", "庚", "辛", "壬", "癸"]
(r, x, y) = (r3, x3, y3)
for i = 1:10
@printf("%s円の半径　%g 中心座標 (%g, %g)\n", name1[i], r, x, y)
circle(x, y, r, i)
circle(x, -y, r, i)
circle(-x, y, r, i)
circle(-x, -y, r, i)
(r, x, y) = nextcircle(r, x, y)
end
name2 = ["乾", "兌", "離", "震", "巽", "坎", "艮", "坤"]
(r, x, y) = (54/7, 270/7, 648/7)
for i = 1:8
@printf("%s円の半径　%g, 中心座標 (%g, %g)\n", name2[i], r, x, y)
circle4(x, y, r, i)
(r, x, y) = nextcircle2(r, x, y)
end
if more
point(0, 0, " O")
point(r1, 0, " r1")
point(R, 0, " R")
point(0, R-r2, " R-r2")
point(x3, y3, "(X3,y3,r3)")
point(50, 25, "天円", mark=false)
point(10, 85, "地円", mark=false)
point(50, 85, "人円", mark=false)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
end
end;

draw(false)

地円の半径 = 36, 人円の半径 = 18
甲円の半径　18, 中心座標 54, 72
乙円の半径　9.818181818181818, 中心座標 78.54545454545455, 58.90909090909091
丙円の半径　5.999999999999991, 中心座標 90.0, 48.0
丁円の半径　4.0, 中心座標 96.0, 40.0
戊円の半径　2.8421052631578947, 中心座標 99.47368421052632, 34.10526315789474
己円の半径　2.117647058823516, 中心座標 101.64705882352943, 29.64705882352941
庚円の半径　1.6363636363636425, 中心座標 103.09090909090908, 26.181818181818187
辛円の半径　1.3012048192770946, 中心座標 104.09638554216873, 23.421686746987955
壬円の半径　1.058823529411749, 中心座標 104.82352941176475, 21.176470588235293
癸円の半径　0.8780487804877857, 中心座標 105.36585365853662, 19.317073170731703
乾円の半径　7.714285714285714, 中心座標 38.57142857142857, 92.57142857142857
兌円の半径　4.153846153846184, 中心座標 29.076923076923112, 99.69230769230774
離円の半径　2.571428571428608, 中心座標 23.142857142857242, 102.85714285714286
震円の半径　1.741935483871028, 中心座標 19.16129032258083, 104.51612903225802
巽円の半径　1.2558139534883404, 中心座標 16.32558139534871, 105.48837209302322
坎円の半径　0.9473684210525465, 中心座標 14.210526315789048, 106.10526315789478
艮円の半径　0.7397260273971918, 中心座標 12.575342465752794, 106.52054794520554
坤円の半径　0.5934065934064815, 中心座標 11.274725274724002, 106.81318681318686