算額（その206） - 算額あれこれ

長野県長野市信更町田野口清水神社文政11年(1828)

中村信弥「改訂増補長野県の算額」県内の算額(P.112)
http://www.wasan.jp/zoho/zoho.html
キーワード：円5個，累円，直角三角形
#Julia #SymPy #算額 #和算 #数学

鈎股弦の中に股，弦に内接し，たがいに外接する全円，天，地，人，末円の 5 円がある。
全円と末円の径がそれぞれ 50 寸，20 寸 4 分 8 厘のとき，鈎，股を求めよ。

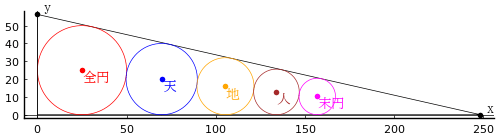
全円，天，地，人，末円の半径をそれぞれ \(r_1,\ r_2,\ r_3,\ r_4,\ r_5\) とおく。また，それぞれの円の中心座標の \(x\) 座標を \(x_1,\ x_2,\ x_3,\ x_4,\ x_5\) とおく。鈎，股の長さを \(y,\ x\) とおく。\(r_1 = 25,\ r_5 = 256/25\) が与えられる。

以下の方程式を立て，nlsolve() で数値解を求める。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms x::positive, y::positive,
x1::positive, x2::positive, x3::positive, x4::positive, x5::positive,
r1::positive, r2::positive, r3::positive, r4::positive, r5::positive;

r1 = 5000 // 200
r5 = 2048 // 200
x1 = r1

eq1 = r1*(x + y + sqrt(x^2 + y^2)) - x*y

eq2 = (x2 - x1)^2 + (r1 - r2)^2 - (r1 + r2)^2
eq3 = (x3 - x2)^2 + (r2 - r3)^2 - (r2 + r3)^2
eq4 = (x4 - x3)^2 + (r3 - r4)^2 - (r3 + r4)^2
eq5 = (x5 - x4)^2 + (r4 - r5)^2 - (r4 + r5)^2

eq6 = r2/(x - x2) - r1/(x - x1)
eq7 = r3/(x - x3) - r1/(x - x1)
eq8 = r4/(x - x4) - r1/(x - x1)
eq9 = r5/(x - x5) - r1/(x - x1);

println(eq1, ",")
println(eq2, ",")
println(eq3, ",")
println(eq4, ",")
println(eq5, ",")
println(eq6, ",")
println(eq7, ",")
println(eq8, ",")
println(eq9, ",")

-x*y + 25*x + 25*y + 25*sqrt(x^2 + y^2),
(25 - r2)^2 - (r2 + 25)^2 + (x2 - 25)^2,
(r2 - r3)^2 - (r2 + r3)^2 + (-x2 + x3)^2,
(r3 - r4)^2 - (r3 + r4)^2 + (-x3 + x4)^2,
(r4 - 256/25)^2 - (r4 + 256/25)^2 + (-x4 + x5)^2,
r2/(x - x2) - 25/(x - 25),
r3/(x - x3) - 25/(x - 25),
r4/(x - x4) - 25/(x - 25),
256/(25*(x - x5)) - 25/(x - 25),

function H(u)
(x, y, x2, r2, x3, r3, x4, r4, x5) = u
return [
-x*y + 25*x + 25*y + 25*sqrt(x^2 + y^2),
(25 - r2)^2 - (r2 + 25)^2 + (x2 - 25)^2,
(r2 - r3)^2 - (r2 + r3)^2 + (-x2 + x3)^2,
(r3 - r4)^2 - (r3 + r4)^2 + (-x3 + x4)^2,
(r4 - 256/25)^2 - (r4 + 256/25)^2 + (-x4 + x5)^2,
r2/(x - x2) - 25/(x - 25),
r3/(x - x3) - 25/(x - 25),
r4/(x - x4) - 25/(x - 25),
256/(25*(x - x5)) - 25/(x - 25),
]
end;

iniv = [big"250.0", # x
55, # y
70, 20, # X2, r2
105, 16, # X3, r3
135, 12, # X4, r4
160] # x5
res = nls(H, ini=iniv)
println(res)

([248.60679774997897, 56.293842981012126, 69.7213595499958, 20.0, 105.49844718999243, 16.0, 134.12011730198975, 12.8, 157.0174533915876], true)

\(x = 248.60680; y = 56.29384\)
\(x1 = 25.00000; r1 = 25.00000\)
\(x2 = 69.72136; r2 = 20.00000\)
\(x3 = 105.49845; r3 = 16.00000\)
\(x4 = 134.12012; r4 = 12.80000\)
\(x5 = 157.01745; r5 = 10.24000\)
\(鈎 = 2.48607, 股 = 0.56294\)

鈎は約2寸4分8厘6毛，股は約5分6厘3毛である。

なお，全円から \(n\) 番目の円の半径は \(25×0.8^n\) である。末円は 4 番目なので，半径は \(25\cdot 0.8^4 = 10.24\) である。

また，半径が求まれば，その円の中心 \(x\) 座標は \(r_i(1-x/25)+x\) ただし，\(x\) は股の長さである。末円の中心 \(x\) 座標は \(10.24(1 - 248.60680/25) + 248.60680 ≒ 157.01745472\) である。

なお，よくあることであるが，算額の図はアスペクト比が実際のものと大きく異なっている。

描画関数プログラムのソースを見る

function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = 5000 // 200
r5 = 2048 // 200
x1 = r1
(x, y, x2, r2, x3, r3, x4, r4, x5) = res[1]
@printf("x = %.5f; y = %.5f; x1 = %.5f; r1 = %.5f; x2 = %.5f; r2 = %.5f; x3 = %.5f; r3 = %.5f; x4 = %.5f; r4 = %.5f; x5 = %.5f; r5 = %.5f\n",
x, y, x1, r1, x2, r2, x3, r3, x4, r4, x5, r5)
@printf("鈎 = %.5f, 股 = %.5f\n", x/100, y/100)
plot([0, x, 0, 0], [0, 0, y, 0], color=:black, lw=0.5)
circle(x1, r1, r1)
circle(x2, r2, r2, :blue)
circle(x3, r3, r3, :orange)
circle(x4, r4, r4, :brown)
circle(x5, r5, r5, :magenta)
if more
point(x1, r1, "全円", :red)
point(x2, r2, "天", :blue)
point(x3, r3, "地", :orange)
point(x4, r4, "人", :brown)
point(x5, r5, "末円", :magenta)
point(0, y, " y", :black, :left, :bottom)
point(x, 0, " x", :black, :left, :bottom)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
end;

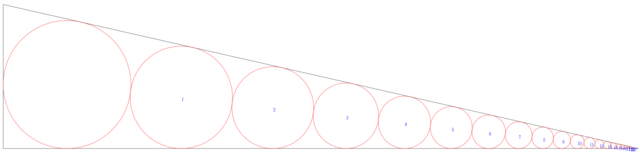
漸化式を用いてたくさんの円を描く。

描画関数プログラムのソースを見る

function draw2()
pyplot(size=(2000, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = 5000 // 200
x1 = r1
(x, y, x2, r2, x3, r3, x4, r4, x5) = res[1]
plot([0, x, 0, 0], [0, 0, y, 0], color=:black, lw=0.5)
circle(x1, r1, r1)
for i in 1:20
ri = 25*0.8^i
xi = ri*(1 - x/25) + x
circle(xi, ri, ri)
point(xi, ri, i, mark=false)
end
plot!(showaxis=false)
end;