算額（その170） - 算額あれこれ

岐阜県大垣市西外側町大垣八幡神社（大垣八幡宮）天保年間

http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF
キーワード：円5個，直線
#Julia #SymPy #算額 #和算 #数学

第29問: 直交するに直線に接し互いに外接する 3 個の等円（赤）を作り，青円と黒円を置く。青円の直径を知って黒円の直径を求めよ。

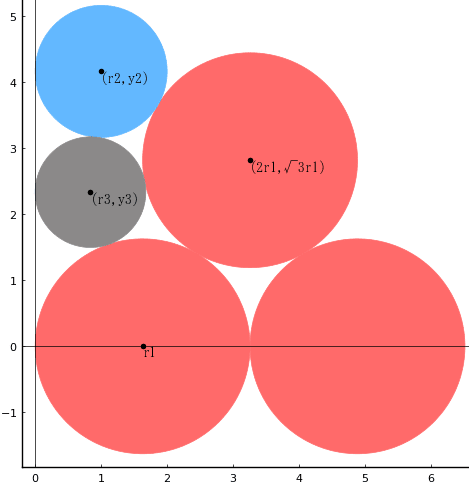
赤円，青円，黒円の直径をそれぞれ \(r_1, r_2, r_3\) として，更に，青円，黒円の中心の \(y\) 座標を \(y_2, y_3\) として連立方程式を解く。なお，2 個の青円の中心が \(x\) 軸になるように座標を定めないと，連立方程式の係数が複雑になり解けないので注意。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms r1::positive, r2::positive, r3::positive, y2::positive, y3::positive;

eq1 = (r1 - r3)^2 + y3^2 - (r1 + r3)^2
eq3 = (2r1 - r3)^2 + (sqrt(Sym(3))r1 - y3)^2 - (r1 + r3)^2
eq4 = (r2 - r3)^2 + (y2 - y3)^2 - (r2 + r3)^2
eq5 = (2r1 - r2)^2 + (y2 - sqrt(Sym(3))r1)^2 - (r1 + r2)^2;

res = solve([eq1, eq3, eq4, eq5], (r1, r3, y2, y3))[1]

(4*sqrt(2)*r2/9 + r2, -2*sqrt(2)*r2 + 11*r2/3, 4*sqrt(6)*r2/9 + 16*sqrt(3)*r2/9, -49*sqrt(3)*r2*(116/441 - 580*sqrt(2)/441)/58)

黒円の半径は \(-2\sqrt{2}r_2 + 11r_2/3\) である。
つまり，「\(黒円の半径 = (11 - 6\sqrt{2})/3 × 青円の半径\)」である。

-2*sqrt(Sym(2))*r2 + 11*r2/3 |> simplify |> println

r2*(11 - 6*sqrt(2))/3

描画関数プログラムのソースを見る

function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r2 = 1 # 青円の半径を 1 として,左右反転した図を描く
(r1, r3, y2, y3) = (4*sqrt(2)*r2/9 + r2, -2*sqrt(2)*r2 + 11*r2/3, 4*sqrt(6)*r2/9 + 16*sqrt(3)*r2/9, -49*sqrt(3)*r2*(116/441 - 580*sqrt(2)/441)/58)
plot()
circle(r1, 0, r1, :indianred1, fill=true)
circle(3r1, 0, r1, :indianred1, fill=true)
circle(2r1, sqrt(3)r1, r1, :indianred1, fill=true)
circle(r2, y2, r2, :steelblue1, fill=true)
circle(r3, y3, r3, :snow4, fill=true)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
if more
point(r2, y2, "(r2,y2)", :black)
point(r3, y3, "(r3,y3)", :black)
point(r1, 0, "r1", :black)
point(2r1, sqrt(3)r1, "(2r1,√3r1)", :black)
end
end;