福島県田村郡三春町平沢担橋 諏訪神社 大正15年(1926)
和算の館
http://www.wasan.jp/fukusima/miharusuwa.html
キーワード:円4個,直線上
#Julia #SymPy #算額 #和算 #数学
直線の上に甲円と乙円が載り,その上に丙円が載っている。甲円,乙円の直径をそれぞれ二寸,三寸としたとき,乙円の直径を求めよ。
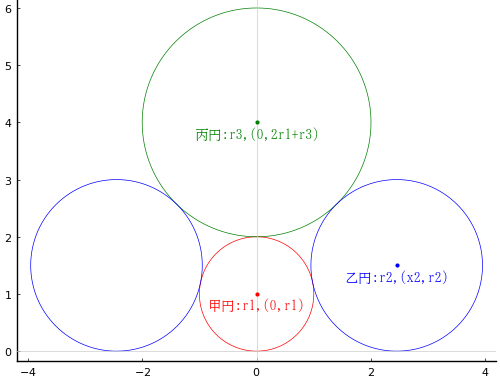
甲円の半径と中心座標を \(r_1,\ (0,\ r_1)\)
乙円の半径と中心座標を \(r_2,\ (x_2,\ r_2)\)
丙円の半径と中心座標を \(r_3,\ (0,\ 2r_1 + r_3)\)
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms r1::positive, r2::positive, x2::positive, r3::positive;
eq1 = x2^2 + (2r1 + r3 - r2)^2 - (r2 + r3)^2
eq2 = x2^2 + (r2 - r1)^2 - (r1 + r2)^2
res = solve([eq1, eq2], (r3, x2))[1]
(-r1^2/(r1 - r2), 2*sqrt(r1)*sqrt(r2))
# r3: 丙円の半径
ans_r3 = res[1]
@show(ans_r3)
ans_r3 = -r1^2/(r1 - r2)
\(\displaystyle - \frac{r_{1}^{2}}{r_{1} - r_{2}}\)
ans_r3(r1 => 2//2, r2 => 3//2)
\(2\)
甲円の直径が 2 寸,乙円の直径が 3 寸のとき,丙円の直径は 4 寸である。
# x2
ans_x2 = res[2]
@show(ans_x2)
ans_x2 = 2*sqrt(r1)*sqrt(r2)
\(2 \sqrt{r_{1}} \sqrt{r_{2}}\)
ans_x2(r1 => 2//2, r2 => 3//2)
\(\sqrt{6}\)
この問題を解くには,算法助術の公式47が応用できる。
\(h = 2r_1 + 2r_3\) とすると,以下の式が成り立つ。
\( (r_1 + r_2) h = 2r_1 r_2 + 2\sqrt{2r_1 r_2 r_3 h}\)
h = 2r1 + 2r3
eq = (r1 + r2)*h - (2r1*r2 + 2sqrt(2r1*r2*r3*h))
ans_r3 = solve(eq, r3)[1]
@show(ans_r3)
ans_r3 = -r1^2/(r1 - r2)
\(\displaystyle - \frac{r_{1}^{2}}{r_{1} - r_{2}}\)
ans_r3(r1 => 2//2, r2 => 3//2)
\(2\)
また,前述の eq2 を解いて \(x_2 = 2\sqrt{r_1 r_2}\) を得るのは最も初歩的な公式である。
描画関数プログラムのソースを見る
function draw(r1, r2, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r3 = r1^2/(r2 - r1)
x2 = 2sqrt(r1*r2)
plot()
circle(0, r1, r1)
circle(0, 2r1 + r3, r3, :green)
circle2(x2, r2, r2, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, 2r1 + r3, "丙円:r3,(0,2r1+r3)", :green, :center, delta=-delta)
point(0, r1, "甲円:r1,(0,r1)", :red, :center, delta=-delta)
point(x2, r2, "乙円:r2,(x2,r2)", :blue, :center, delta=-delta)
end
end;
draw(2/2, 3/2, true)
以下のアイコンをクリックして応援してください