算額（その76） - 算額あれこれ

大阪府茨木市井於神社弘化3年(1846)

和算の館
http://www.wasan.jp/osaka/iyo.html
キーワード：円1個，三角形
#Julia #SymPy #算額 #和算 #数学

一般の三角形（不等辺三角形）において，辺の長い順に大斜，中斜，小斜という。それぞれが 4 寸，2 寸 7 分，1 寸 8 分であるとき，内接する円の直径を求めよ。

内接円の半径を \(r\)，三角形の面積を \(S\) とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms 大斜::positive, 中斜::positive, 小斜::positive,
r::positive, s::positive, S::positive;
s = (大斜 + 中斜 + 小斜)//2
eq1 = (大斜 + 中斜 + 小斜)*r//2 - S
eq2 = sqrt(Sym(s) * (s - 大斜) * (s - 中斜) * (s - 小斜)) - S
res = solve([eq1, eq2])[1]

\begin{equation*}\begin{cases}S & \text{=>} &\frac{\sqrt{- 中斜^{4} + 2 中斜^{2} 大斜^{2} + 2 中斜^{2} 小斜^{2} - 大斜^{4} + 2 大斜^{2} 小斜^{2} - 小斜^{4}}}{4}\\r & \text{=>} &\frac{\sqrt{- 中斜^{4} + 2 中斜^{2} 大斜^{2} + 2 中斜^{2} 小斜^{2} - 大斜^{4} + 2 大斜^{2} 小斜^{2} - 小斜^{4}}}{2 \left(中斜 + 大斜 + 小斜\right)}\\\end{cases}\end{equation*}

# r: 内接円の半径
@show(res[r])

res[r] = sqrt(-中斜^4 + 2*中斜^2*大斜^2 + 2*中斜^2*小斜^2 - 大斜^4 + 2*大斜^2*小斜^2 - 小斜^4)/(2*(中斜 + 大斜 + 小斜))

\(\displaystyle \frac{\sqrt{- 中斜^{4} + 2 中斜^{2} 大斜^{2} + 2 中斜^{2} 小斜^{2} - 大斜^{4} + 2 大斜^{2} 小斜^{2} - 小斜^{4}}}{2 \left(中斜 + 大斜 + 小斜\right)}\)

根号の中身は因数分解できるので，少し簡単になる。

ans_r = res[r]^2 |> factor |> sqrt

\(\displaystyle \frac{\sqrt{- \left(中斜 - 大斜 - 小斜\right) \left(中斜 - 大斜 + 小斜\right) \left(中斜 + 大斜 - 小斜\right)}}{2 \sqrt{中斜 + 大斜 + 小斜}}\)

res[r](大斜 => 4, 中斜 => 2.7, 小斜 => 1.8) * 2

\(0.9452668468558\)

ans_r(大斜 => 4, 中斜 => 2.7, 小斜 => 1.8) * 2

\(0.9452668468558\)

大斜，中斜，小斜が 4 寸，2 寸 7 分，1 寸 8 分であるとき，内接する円の直径は 9分4厘5毛である。

算額では，径は 1寸7厘5毛となっている。

どちらが正しいか，図を描いて確かめると，得られた解で正しいようである。算額における三角形とは随分異なる。

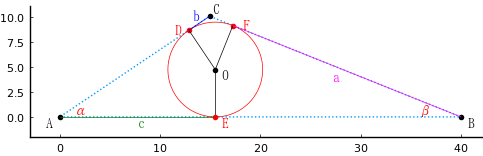
図を描くには，\(BF = a,\ CD = b,\ AE = c,\ ∠CAB = \alpha,\ ∠ABC = \beta\) として，プログラム中で必要な座標を計算する。

なお，本問は算法助術の公式36 そのものである。
公式36は図に示す \(a,\ b,\ c\) を用い，内接円の半径 \(r\) において，\(r^2(a + b + c) = a b c\) の関係式が成り立つ。
これは，ヘロンの公式そのものである。

@syms a, b, c, 大斜, 中斜, 小斜
eq1 = 大斜 - (a + b)
eq2 = 中斜 - (a + c)
eq3 = 小斜 - (b + c)
eq4 = r^2*(a + b + c) - a*b*c
res = solve([eq1, eq2, eq3, eq4], (r, a, b, c))[2]

(sqrt(-(中斜 - 大斜 - 小斜)*(中斜 - 大斜 + 小斜)*(中斜 + 大斜 - 小斜)/(中斜 + 大斜 + 小斜))/2, (中斜 + 大斜 - 小斜)/2, -(中斜 - 大斜 - 小斜)/2, (中斜 - 大斜 + 小斜)/2)

# r: 内接円の半径
@show(res[1])

res[1] = sqrt(-(中斜 - 大斜 - 小斜)*(中斜 - 大斜 + 小斜)*(中斜 + 大斜 - 小斜)/(中斜 + 大斜 + 小斜))/2

\(\displaystyle \frac{\sqrt{- \frac{\left(中斜 - 大斜 - 小斜\right) \left(中斜 - 大斜 + 小斜\right) \left(中斜 + 大斜 - 小斜\right)}{中斜 + 大斜 + 小斜}}}{2}\)

前述した解と同じものが得られる。

res[1](大斜 => 4, 中斜 => 2.7, 小斜 => 1.8).evalf() * 2

\(0.9452668468558\)

描画関数プログラムのソースを見る

function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(大斜, 中斜, 小斜) = (40, 27, 18)
α = acos( (小斜^2 + 大斜^2 - 中斜^2) / (2*小斜*大斜))
β = acos( (中斜^2 + 大斜^2 - 小斜^2) / (2*中斜*大斜))
a = 中斜/2 + 大斜/2 - 小斜/2
b = 中斜/2 - 大斜/2 + 小斜/2
c = -中斜/2 + 大斜/2 + 小斜/2
s = (大斜 + 中斜 + 小斜)/2
S = sqrt(s * (s - 大斜) * (s - 中斜) * (s - 小斜))
r = 2S/(大斜 + 中斜 + 小斜)
plot([0, 大斜, 小斜*cos(α), 0], [0, 0, 小斜*sin(α), 0],
lwd=0.25, linestyle=more ? :dot : :solid,
xlims=(-3, 大斜+3), ylims=(-2, 小斜*sin(α)+1))
circle(c, r, r)
if more
println("直径 = ", 2r)
point(0, 0, " α", :red, :bottom, :left, mark=false)
point(大斜, 0, "β ", :red, :bottom, :right, mark=false)
segment(c, 0, c, r)
point(c, r, " O", :black)
point(c*cos(α), c*sin(α), "D ", :red, :center, :right)
segment(c*cos(α), c*sin(α), c, r)
point(c, 0, " E", :red, :top, :center)
point(大斜 - a*cos(β), a*sin(β), " F", :red, :center)
segment(大斜 - a*cos(β), a*sin(β), c, r)
point(0, 0, "A ", :black, :right)
point(大斜, 0, " B", :black)
point(小斜*cos(α), 小斜*sin(α), " C", :black, :bottom)
segment(0, 0, c, 0, :green)
point(c/2, 0, "c", :green, mark=false)
segment(大斜, 0, 大斜 - a*cos(β), a*sin(β), :magenta)
point(大斜 - a*cos(β)/2, a*sin(β)/2, "a ", :magenta, :right, mark=false)
segment(小斜*cos(α), 小斜*sin(α), c*cos(α), c*sin(α), :blue)
point( (小斜 + c)*cos(α)/2, (小斜+c)*sin(α)/2, "b", :blue, :bottom, :right, mark=false)
end
end;