算額（その69） - 算額あれこれ

長野県長野市篠井長谷観音堂享和3年(1803)

中村信弥「改訂増補長野県の算額」県内の算額(P.73)
http://www.wasan.jp/zoho/zoho.html
キーワード：円2個，直角三角形
#Julia #SymPy #算額 #和算 #数学

直角三角形の中に大円と小円が斜線で区切られて入っている。大円，小円の径がそれぞれ 32 尺，24 尺である。鉤，股，弦を求めよ。

注：直角三角形の直角を挟む短い辺（鉤）と長い辺（股）と直角に対する辺（弦）。弦に下ろした垂線は中鈎，中鈎と弦の交点で区切られる弦は長弦と短弦。

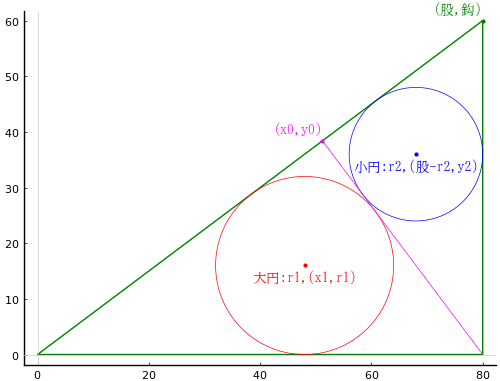
鈎股弦，中鈎，短弦，長弦をそのまま変数名とする。
大円の半径と中心座標を \(r_1,\ (x_1,\ r_1)\)
小円の半径と中心座標を \(r_2,\ (股 - r_2,\ y_2)\)
とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms r1::positive, r2::positive,
鈎::positive, 股::positive, 弦::positive,
中鈎::positive, 長弦::positive, 短弦::positive;
eq1 = 中鈎^2 + 長弦^2 - 股^2
eq2 = 中鈎^2 + 短弦^2 - 鈎^2
eq3 = r1/r2 - 股/鈎
eq4 = r1/r2 - 長弦/中鈎
eq5 = 長弦 + 中鈎 - 股 - 2r1
eq6 = 弦^2 - (鈎^2 + 股^2)
# eq6 = 短弦 + 中鈎 - 鈎 - 2r2
res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (鈎, 股, 弦, 中鈎, 長弦, 短弦))[3] # 3 of 3

( (r1*(r1 + sqrt(r1^2 + r2^2)) + r2^2 + r2*sqrt(r1^2 + r2^2))/r1, (r1^2 + r1*sqrt(r1^2 + r2^2) + r2*(r2 + sqrt(r1^2 + r2^2)))/r2, sqrt(2)*sqrt(r1^5*(r1 + sqrt(r1^2 + r2^2)) + r1^4*r2*(r1 + sqrt(r1^2 + r2^2)) + r1^2*r2^2*(3*r1^2 + 2*r1*r2 + 2*r1*sqrt(r1^2 + r2^2) + 3*r2^2 + 2*r2*sqrt(r1^2 + r2^2)) + r1*r2^4*(r2 + sqrt(r1^2 + r2^2)) + r2^5*(r2 + sqrt(r1^2 + r2^2)))/(r1*r2), r1 + r2 + sqrt(r1^2 + r2^2), r1*(r1 + r2 + sqrt(r1^2 + r2^2))/r2, r2*(r1 + r2 + sqrt(r1^2 + r2^2))/r1)

それぞれの式のあとに示すのは，大円，小円の直径が 32 寸，24 寸のときの値。

# 鈎
ans_鈎 = res[1]
@show(ans_鈎)

ans_鈎 = (r1*(r1 + sqrt(r1^2 + r2^2)) + r2^2 + r2*sqrt(r1^2 + r2^2))/r1

\(\displaystyle \frac{r_{1} \left(r_{1} + \sqrt{r_{1}^{2} + r_{2}^{2}}\right) + r_{2}^{2} + r_{2} \sqrt{r_{1}^{2} + r_{2}^{2}}}{r_{1}}\)

ans_鈎(r1 => 32//2, r2 => 24//2)

\(60\)

# 股
ans_股 = res[2]
@show(ans_股)

ans_股 = (r1^2 + r1*sqrt(r1^2 + r2^2) + r2*(r2 + sqrt(r1^2 + r2^2)))/r2

\(\displaystyle \frac{r_{1}^{2} + r_{1} \sqrt{r_{1}^{2} + r_{2}^{2}} + r_{2} \left(r_{2} + \sqrt{r_{1}^{2} + r_{2}^{2}}\right)}{r_{2}}\)

ans_股(r1 => 32//2, r2 => 24//2)

\(80\)

# 弦
ans_弦 = res[3] |> factor
@show(ans_弦)

ans_弦 = sqrt(2)*(r1^2 + r2^2)*sqrt(r1^2 + r1*r2 + r1*sqrt(r1^2 + r2^2) + r2^2 + r2*sqrt(r1^2 + r2^2))/(r1*r2)

\(\displaystyle \frac{\sqrt{2} \left(r_{1}^{2} + r_{2}^{2}\right) \sqrt{r_{1}^{2} + r_{1} r_{2} + r_{1} \sqrt{r_{1}^{2} + r_{2}^{2}} + r_{2}^{2} + r_{2} \sqrt{r_{1}^{2} + r_{2}^{2}}}}{r_{1} r_{2}}\)

ans_弦(r1 => 32//2, r2 => 24//2)

\(100\)

# 中鈎
ans_中鈎 = res[4]
@show(ans_中鈎)

ans_中鈎 = r1 + r2 + sqrt(r1^2 + r2^2)

\(r_{1} + r_{2} + \sqrt{r_{1}^{2} + r_{2}^{2}}\)

ans_中鈎(r1 => 32//2, r2 => 24//2)

\(48\)

# 長弦
ans_長弦 = res[5]
@show(ans_長弦)

ans_長弦 = r1*(r1 + r2 + sqrt(r1^2 + r2^2))/r2

\(\displaystyle \frac{r_{1} \left(r_{1} + r_{2} + \sqrt{r_{1}^{2} + r_{2}^{2}}\right)}{r_{2}}\)

ans_長弦(r1 => 32//2, r2 => 24//2)

\(64\)

# 短弦
ans_短弦 = res[6]
@show(ans_短弦)

ans_短弦 = r2*(r1 + r2 + sqrt(r1^2 + r2^2))/r1

\(\displaystyle \frac{r_{2} \left(r_{1} + r_{2} + \sqrt{r_{1}^{2} + r_{2}^{2}}\right)}{r_{1}}\)

ans_短弦(r1 => 32//2, r2 => 24//2)

\(36\)

描画関数プログラムのソースを見る

function draw(r1, r2, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
t = sqrt(r1^2 + r2^2)
u = r2*(r2 + t)
鈎 = (r1*(r1 + t) + u)/r1
股 = (r1*(r1 + t) + u)/r2
中鈎 = r1 + r2 + t
弦 = √2t^2*sqrt(r1*中鈎 + u)/(r1*r2)
長弦 = 中鈎*r1/r2
短弦 = 中鈎*r2/r1
x1 = r1/tan(atan(鈎/股)/2)
y2 = 鈎 - r2/tan(atan(股/鈎)/2)
x0 = 股 - 中鈎*鈎/弦
y0 = 中鈎*股/弦
println( (股, 鈎, 中鈎, 長弦, 短弦, x1, y2))
plot([0, 股, 股, 0], [0, 0, 鈎, 0], color=:green)
circle(x1, r1, r1)
circle(股 - r2, y2, r2, :blue)
segment(股, 0, x0, y0, :magenta)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x1, r1, "大円:r1,(x1,r1)", :red, :center, delta=-delta)
point(股 - r2, y2, "小円:r2,(股-r2,y2)", :blue, :center, delta=-delta)
point(x0, y0, "(x0,y0)", :magenta, :right, :bottom, delta=delta)
point(股, 鈎, "(股,鈎)", :green, :right, :bottom, delta=delta)
end
end;
draw(32/2, 24/2, true)