新潟県三島郡 与板八幡宮 寛政12年(1800)
和算の館 新潟県柏崎市与板 与板三柱神社 であろう
http://www.wasan.jp/niigata/yoitahatiman1.html
キーワード:累円,直線上
#Julia #SymPy #算額 #和算 #数学
直線と互いに接する大円と小円があり,更に小円と大円と直線に接する連続する小円がある。大円の径が10寸,一番小さい小円の径が1分のとき,小円の数はいくつか。
大円の半径を \(R\),大きい方から 2 つの小円の半径と中心の \(x\) 座標を \(r_1,\ x_1,\ r_2,\ x_2\) と置き,以下の方程式を立てる。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms R::positive, r1::positive, r2::positive, x1::positive, x2::positive;
R = 1
eq1 = x1^2 + (R - r1)^2 - (R + r1)^2;
eq2 = x2^2 + (R - r2)^2 - (R + r2)^2;
eq3 = (x1 - x2)^2 + (r1 - r2)^2 - (r1 + r2)^2;
一番大きい小円の中心の \(x\) 座標は,eq1 を \(x_1\) について解けば求まる。
solve(eq1, x1)
2*sqrt(r1)
eq1, eq2, eq3 を \(r_2,\ x_2\) について解けば,ある小円の次に小さい小円の半径と中心の \(x\) 座標を求める漸化式が得られる。
res = solve([eq1, eq2, eq3], (r2, x2))[1]. # 1 of 2
(x1*(-2*sqrt(r1)*x1/(r1 - 1) + x1 + 2*x1/(r1 - 1))/(4*(r1 - 1)), sqrt(r1)*x1/(r1 - 1) - x1/(r1 - 1))
res[1] |> simplify |> println # r2
x1^2*(-2*sqrt(r1) + r1 + 1)/(4*(r1 - 1)^2)
res[2] |> simplify |> println # x2
x1*(sqrt(r1) - 1)/(r1 - 1)
小円 \( (r_1,\ x_1)\) から次の小円 \( (r_2,\ x_2)\) を得る関数を書く。
function nextcircle(r1, x1; R = 1)
r2 = x1^2*(-2*sqrt(r1) + r1 + 1)/(4*(r1 - 1)^2)
x2 = x1*(sqrt(r1) - 1)/(r1 - 1)
return r2, x2
end;
この関数を使い,初期値を 1 にするとエラーになるが,1 に極めて近い値を設定することで 10 番目の小円の半径が大円のほぼ 1/100 = 0.01 になることがわかる。
r = 0.99999 # r1
x = 2sqrt(r) # x1
for i = 2:10
r, x = nextcircle(r, x)
@printf("%g, %g, %g\n", i, r, x)
end
2, 0.2499986308990838, 0.999997499986309
3, 0.11111075838251418, 0.6666656084800361
4, 0.062499851192534595, 0.499999404769784
5, 0.03999992381055049, 0.399999619052571
6, 0.027777733686650655, 0.3333330687864656
7, 0.020408135499460415, 0.28571409135329967
8, 0.015624981399050211, 0.24999985119235743
9, 0.012345665948302833, 0.22222210464580552
10, 0.009999990476312013, 0.19999990476309745
図示することで,正しく描画されることを確認する。
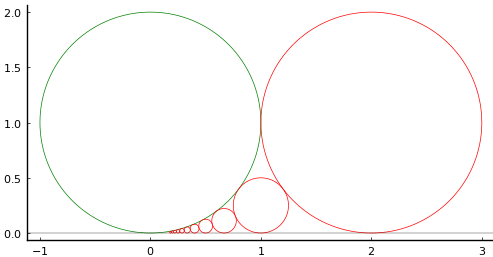
描画関数プログラムのソースを見る
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
R = 1
plot()
circle(0, R, R, :green)
r = 0.99999 # r1
x = 2sqrt(r) # x1
circle(x, r, r)
for i = 2:11
r, x = nextcircle(r, x, R=R)
@printf("%d, r = %g, x = %g\n", i, r, x)
circle(x, r, r)
end
hline!([0], color=:black, linewidth=0.25)
if more
point(0, 0, "0 ", :black, :right)
point(0, r3, "r3 ", :black, :right)
point(0, r3+r1, "r3+r1 ", :blue, :right)
point(0, 1-r2, "1-r2 ", :red, :right)
point(x4, r4, "(x4,r4)", :magenta, :center)
vline!([0], color=:black, linewidth=0.25)
hline!([0], color=:black, linewidth=0.25)
end
end;
draw(false)
2, r = 0.2499986308990838, x = 0.999997499986309
3, r = 0.11111075838251418, x = 0.6666656084800361
4, r = 0.062499851192534595, x = 0.499999404769784
5, r = 0.03999992381055049, x = 0.399999619052571
6, r = 0.027777733686650655, x = 0.3333330687864656
7, r = 0.020408135499460415, x = 0.28571409135329967
8, r = 0.015624981399050211, x = 0.24999985119235743
9, r = 0.012345665948302833, x = 0.22222210464580552
10, r = 0.009999990476312013, x = 0.19999990476309745
11, r = 0.008264455654629146, x = 0.18181810310999452
-----------
先の方程式を,小円 r2, x2 から次に大きい小円 r1, x1 を求める漸化式を作るように解くと以下のようになる。
using SymPy
@syms R::positive, r1::positive, r2::positive, x1::positive, x2::positive;
R = 1
eq1 = x1^2 + (R - r1)^2 - (R + r1)^2;
eq2 = x2^2 + (R - r2)^2 - (R + r2)^2;
eq3 = (x1 - x2)^2 + (r1 - r2)^2 - (r1 + r2)^2;
solve(eq2, x2)
2*sqrt(r2)
res = solve([eq1, eq2, eq3], (r1, x1))
2-element Vector{Tuple{Sym, Sym}}:
(-x2*(-2*sqrt(r2)*x2/(r2 - 1) - x2 - 2*x2/(r2 - 1))/(4*(r2 - 1)), -sqrt(r2)*x2/(r2 - 1) - x2/(r2 - 1))
(-x2*(2*sqrt(r2)*x2/(r2 - 1) - x2 - 2*x2/(r2 - 1))/(4*(r2 - 1)), sqrt(r2)*x2/(r2 - 1) - x2/(r2 - 1))
function nextcircle(r2, x2; R = 1)
r = -x2*(-2*sqrt(r2)*x2/(r2 - 1) - x2 - 2*x2/(r2 - 1))/(4*(r2 - 1))
x = -sqrt(r2)*x2/(r2 - 1) - x2/(r2 - 1)
return r, x
end;
この漸化式によれば,半径が 0.01 からスタートして 10 番目の小円の半径がほぼ 1 になることが確認できる。
r = 0.01 # r1
x = 2sqrt(r) # x1
for i = 2:10
r, x = nextcircle(r, x)
@printf("%g, %g, %g\n", i, r, x)
end
2, 0.012345679012345682, 0.22222222222222227
3, 0.01562500000000001, 0.25000000000000006
4, 0.02040816326530613, 0.28571428571428575
5, 0.02777777777777779, 0.3333333333333334
6, 0.04000000000000003, 0.40000000000000013
7, 0.06250000000000006, 0.5000000000000002
8, 0.1111111111111112, 0.666666666666667
9, 0.25000000000000033, 1.0000000000000007
10, 1.0000000000000027, 2.0000000000000027
描画関数プログラムのソースを見る
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
R = 1
plot()
circle(0, R, R, :green)
r = 0.01 # r1
x = 2sqrt(r) # x1
circle(x, r, r)
@printf("1, r = %g x = %g\n", r, x)
for i = 2:10
r, x = nextcircle(r, x, R=R)
@printf("%d, r = %g, x = %g\n", i, r, x)
circle(x, r, r)
end
hline!([0], color=:black, linewidth=0.25)
if more
point(0, 0, "0 ", :black, :right)
point(0, r3, "r3 ", :black, :right)
point(0, r3+r1, "r3+r1 ", :blue, :right)
point(0, 1-r2, "1-r2 ", :red, :right)
point(x4, r4, "(x4,r4)", :magenta, :center)
vline!([0], color=:black, linewidth=0.25)
hline!([0], color=:black, linewidth=0.25)
end
end;
draw(false)
1, r = 0.01, x = 0.2
2, r = 0.012345679012345682, x = 0.22222222222222227
3, r = 0.01562500000000001, x = 0.25000000000000006
4, r = 0.02040816326530613, x = 0.28571428571428575
5, r = 0.02777777777777779, x = 0.3333333333333334
6, r = 0.04000000000000003, x = 0.40000000000000013
7, r = 0.06250000000000006, x = 0.5000000000000002
8, r = 0.1111111111111112, x = 0.666666666666667
9, r = 0.25000000000000033, x = 1.0000000000000007
10, r = 1.0000000000000027, x = 2.0000000000000027
二番目に小さい小円の半径が 0.012345679012345682(≒ 1/81) というのは,意味深だなあ。
と書いたまま放っておいたのだが,よくよく見てみたら \(\displaystyle \frac{1}{n^2}\) という数列だ。
以下のアイコンをクリックして応援してください