算額（その40） - 算額あれこれ

神奈川県川崎市多摩区須賀神社祖師堂文政6年(1823)

和算の館
http://www.wasan.jp/kanagawa/suga.html
キーワード：円4個，外円，正三角形，正方形
#Julia #SymPy #算額 #和算 #数学

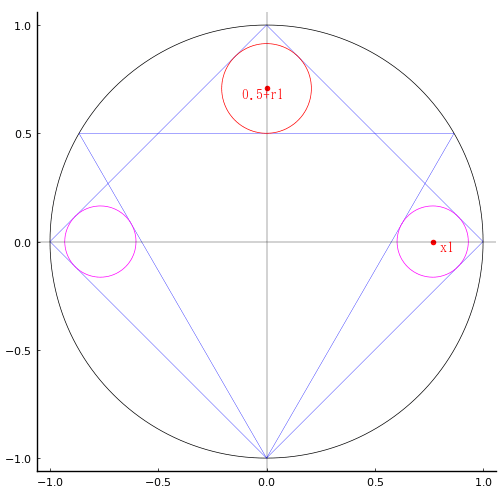
外円の中に正方形，正三角形，2 種類の小円が収まっている。各小円の径を求めよ。

外円の半径を 1 とし，以下のように記号を定め，方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms r1::positive, r2::positive, x1::positive;

# 上部にある円の半径: -1/2 + sqrt(2)/2
r1 = solve(sqrt(Sym(2))r1 + r1 - 1//2)[1]
r1 |> println

-1/2 + sqrt(2)/2

# 左右にある円の半径と中心座標
eq4 = (x1 + r2/sqrt(Sym(2))) - x1 - (1-(x1 + r2/sqrt(Sym(2))))
eq5 = x1 - 1/sqrt(Sym(3)) - 2r2/sqrt(Sym(3))
res = solve([eq4, eq5], (r2, x1));

# 半径
res[r2] |> println

-sqrt(3) - sqrt(6)/2 + 1 + 3*sqrt(2)/2

# 円の中心の x 座標
res[x1] |> println

-2 - sqrt(2) + sqrt(3) + sqrt(6)

描画関数プログラムのソースを見る

radian(degree) = degree / 180 * π;

function plotpolygon2(ox, oy, r, n; φ=90, col=:black, lty=:solid, lwd=1, fcol="")
θ = range(0, 2π, length=n+1) .+ radian(φ)
if fcol == ""
plot!(r .* cos.(θ) .+ ox, r .* sin.(θ) .+ oy,
linecolor=col, linestyle=lty, linewidth=lwd)
else
plot!(r .* cos.(θ) .+ ox, r .* sin.(θ) .+ oy,
linecolor=col, linestyle=lty, linewidth=lwd,
seriestype=:shape, fillcolor=fcol)
end
end;

function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
plot()
circle(0, 0, 1, :black)
plotpolygon2(0, 0, 1, 3, φ=150, lwd=0.25, col=:blue)
plotpolygon2(0, 0, 1, 4, φ=90, lwd=0.25, col=:blue)
r1 = (sqrt(2)-1)/2
circle(0, 0.5+r1, r1)
r2 = -sqrt(3) - sqrt(6)/2 + 1 + 3*sqrt(2)/2
x1 = -2 - sqrt(2) + sqrt(3) + sqrt(6)
circle2(x1, 0, r2, :magenta)
if more
point(0, 0.5+r1, "0.5+r1 ", :red, :center)
point(x1, 0, " x1", :red, :left)
vline!([0], color=:black, linewidth=0.25)
hline!([0], color=:black, linewidth=0.25)
end
end;