兵庫県姫路市広田区北野町 英賀天満宮 奉納年不明(明治6年より前)
愛媛和算研究会:司馬遼太郎の祖父惣八の算額
https://ehimewasan.com/archives/1651
https://ehimewasan.com/wp-content/uploads/2024/11/a56924317999746a755154fca5db036d.pdf
キーワード:円6個,正方形
#Julia #SymPy #算額 #和算 #数学
正方形の中に甲円 2 個,乙円 4 個を容れる。乙円の直径が 1 寸のとき,甲円の直径はいかほどか。
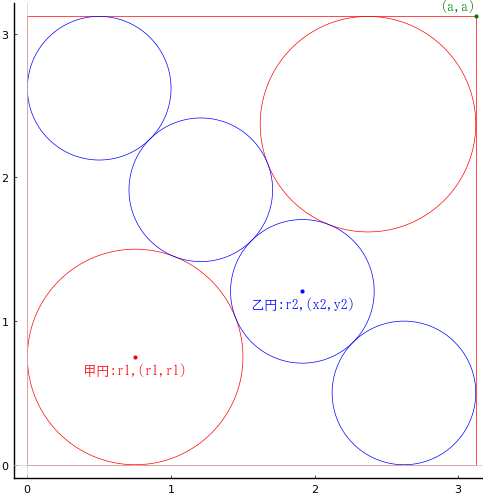
正方形の一辺の長さを \(a\)
甲円の半径と中心座標を \(r_1,\ (r_1,\ r_1)\)
乙円の半径と中心座標を \(r_2,\ (x_2,\ y_2)\)
とおき,以下の連立方程式を解く。
なお,
\(x_2 = a - (\sqrt{2} + 2)r_2\)
\(y_2 = (\sqrt{2} + 2)r_2\)
である。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms a, r1, r2
x2 = (1 + 2√Sym(2))r2
y2 = a - x2
eq1 = √Sym(2)a - (6 + 2√Sym(2))*r2
eq2 = (x2 - r1)^2 + (y2 - r1)^2 - (r1 + r2)^2
res = solve([eq1, eq2], (r1, a))[1] # 1 of 2
(-2*r2*sqrt(4 + 3*sqrt(2)) + 3*r2*(1 + sqrt(2)), r2*(2 + 3*sqrt(2)))
# r1
ans_r1 = res[1] |> factor
\(r_{2} \left(- 2 \sqrt{4 + 3 \sqrt{2}} + 3 + 3 \sqrt{2}\right)\)
術は一時変数を使っているので簡単な式に見えるが,最終的には同じ数式になる。
「術曰置二個開平方加一個三之各(名)極加一個開平方倍之以減極餘乗乙径得甲径合問
# 術
@syms 乙円径, 極
極 = 3(√Sym(2) + 1)
甲円径 = (極 - sqrt(極 + 1)*2)*乙円径
甲円径 |> factor
\(乙円径 \left(- 2 \sqrt{4 + 3 \sqrt{2}} + 3 + 3 \sqrt{2}\right)\)
乙円の直径が 1 寸のとき,甲円の直径は 1.50064079609898 寸である。
ans_r1(r2 => 1/2).evalf() * 2
\(1.50064079609898\)
# a: 正方形の一辺の長さ
ans_a = res[2]
\(r_{2} \left(2 + 3 \sqrt{2}\right)\)
乙円の直径が 1 のとき,正方形の一辺の長さは 3.12132034355964 である。
ans_a(r2 => 1/2).evalf()
\(3.12132034355964\)
描画関数プログラムのソースを見る
function draw(r2, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = r2*(3 + 3√2 - 2sqrt(4 + 3√2))
a = r2*(2 + 3√2)
x2 = r2*(1 + 2√2)
y2 = a - x2
println( (2r1, a))
plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:red, lw=0.5)
circle(r1, r1, r1)
circle(a - r1, a - r1, r1)
for i = 0:3
circle(r2 + i*√2*r2, a - (1 + i*√2)r2, r2, :blue)
end
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(a, a, "(a,a)", :green, :right, :bottom, delta=delta/2)
point(r1, r1, "甲円:r1,(r1,r1)", :red, :center, delta=-delta)
point(x2, y2, "乙円:r2,(x2,y2)", :blue, :center, delta=-delta)
end
end;
draw(1/2, true)
(1.5006407960989856, 3.121320343559643)
以下のアイコンをクリックして応援してください