安島直円:不朽算法(上巻)
東北大学総合知デジタルアーカイブ
https://touda.tohoku.ac.jp/portal/item/10010000022977
キーワード:円4個,三角形
#Julia #SymPy #算額 #和算 #数学
第十五 (不等辺)三角形の中に,甲円,乙円,丙円,丁円を容れる。甲円,乙円,丙円は三角形の 2 辺に接し,丁円は底辺に接している。隣り合う円は互いに外接している。三角形の 3 辺の長さが与えられたとき,各円の直径はいかほどか。
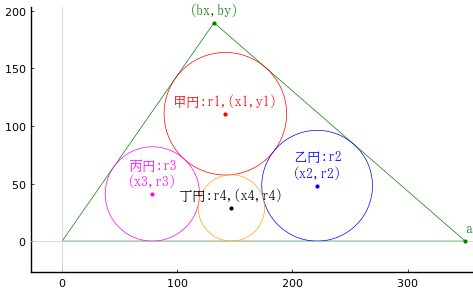
三角形の辺,底辺(下斜),斜辺(右斜,左斜) を \(a,\ b,\ c;\ a ≧ b ≧ c\)とする
下斜の左頂点が原点 \( (0,\ 0)\),右頂点が \( (a, 0)\) になるように座標を定める。
三角形の頂点座標は \(a,\ b,\ c\) により決まるが,これを \( (b_x,\ b_y)\)
甲円の半径と中心座標を \(r_1,\ (x_1,\ y_1)\)
乙円の半径と中心座標を \(r_2,\ (x_2,\ r_2)\)
丙円の半径と中心座標を \(r_3,\ (x_3,\ r_3)\)
丁円の半径と中心座標を \(r_4,\ (x_4,\ r_3)\)
とおき,以下の方程式の数値解を求める。
結論を先に書いておく。
算額の問は「左斜が 231 寸,右斜が 289 寸,下斜が 350 寸のとき,甲円径はいかほどか」で,答えは「甲円径 112 寸」となっている。
この答えは間違いである。GeoGebra などで描いてみると,円の外接関係に齟齬が出る。
正しい答えは,甲円径 = 106.402097379784 寸,乙円径 = 96.1612747886687 寸,丙円径 = 81.9018220754186 寸,丁円径 = 57.5587526228188 である(上の図は,このときのもの)。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms a::positive, b::positive, c::positive,
bx::positive, by::positive,
r1::positive, x1::positive, y1::positive,
r2::positive, x2::positive,
r3::positive, x3::positive,
r4::positive, x4::positive
eq1 = bx^2 + by^2 - c^2
eq2 = (a - bx)^2 + by^2 - b^2
eq3 = (x1 - x2)^2 + (y1 - r2)^2 - (r1 + r2)^2
eq4 = (x1 - x3)^2 + (y1 - r3)^2 - (r1 + r3)^2
eq5 = (x1 - x4)^2 + (y1 - r4)^2 - (r1 + r4)^2
eq6 = (x2 - x4)^2 + (r2 - r4)^2 - (r2 + r4)^2
eq7 = (x3 - x4)^2 + (r3 - r4)^2 - (r3 + r4)^2
eq8 = dist2(0, 0, bx, by, x1, y1, r1)
eq9 = dist2(0, 0, bx, by, x3, r3, r3)
eq10 = dist2(a, 0, bx, by, x1, y1, r1)
eq11 = dist2(a, 0, bx, by, x2, r2, r2);
#res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9], (bx, by, r1, x1, r2, x2, r3, x3, y3))
solve([eq1, eq2], (bx, by))[1]
( (a^2 - b^2 + c^2)/(2*a), sqrt(-(a - b - c)*(a - b + c)*(a + b - c))*sqrt(a + b + c)/(2*a))
println(eq3, ", # eq3")
println(eq4, ", # eq4")
println(eq5, ", # eq5")
println(eq6, ", # eq6")
println(eq7, ", # eq7")
println(eq8, ", # eq8")
println(eq9, ", # eq9")
println(eq10, ", # eq10")
println(eq11, ", # eq11")
-(r1 + r2)^2 + (-r2 + y1)^2 + (x1 - x2)^2, # eq3
-(r1 + r3)^2 + (-r3 + y1)^2 + (x1 - x3)^2, # eq4
-(r1 + r4)^2 + (-r4 + y1)^2 + (x1 - x4)^2, # eq5
(r2 - r4)^2 - (r2 + r4)^2 + (x2 - x4)^2, # eq6
(r3 - r4)^2 - (r3 + r4)^2 + (x3 - x4)^2, # eq7
-bx^2*r1^2 + bx^2*y1^2 - 2*bx*by*x1*y1 - by^2*r1^2 + by^2*x1^2, # eq8
by*(-2*bx*r3*x3 - by*r3^2 + by*x3^2), # eq9
a^2*by^2 - 2*a^2*by*y1 - a^2*r1^2 + a^2*y1^2 + 2*a*bx*by*y1 + 2*a*bx*r1^2 - 2*a*bx*y1^2 - 2*a*by^2*x1 + 2*a*by*x1*y1 - bx^2*r1^2 + bx^2*y1^2 - 2*bx*by*x1*y1 - by^2*r1^2 + by^2*x1^2, # eq10
by*(a^2*by - 2*a^2*r2 + 2*a*bx*r2 - 2*a*by*x2 + 2*a*r2*x2 - 2*bx*r2*x2 - by*r2^2 + by*x2^2), # eq11
function driver(arg_a, arg_b, arg_c)
function H(u)
(r1, x1, y1, r2, x2, r3, x3, r4, x4) = u
return [
-(r1 + r2)^2 + (-r2 + y1)^2 + (x1 - x2)^2, # eq3
-(r1 + r3)^2 + (-r3 + y1)^2 + (x1 - x3)^2, # eq4
-(r1 + r4)^2 + (-r4 + y1)^2 + (x1 - x4)^2, # eq5
(r2 - r4)^2 - (r2 + r4)^2 + (x2 - x4)^2, # eq6
(r3 - r4)^2 - (r3 + r4)^2 + (x3 - x4)^2, # eq7
-bx^2*r1^2 + bx^2*y1^2 - 2*bx*by*x1*y1 - by^2*r1^2 + by^2*x1^2, # eq8
by*(-2*bx*r3*x3 - by*r3^2 + by*x3^2), # eq9
a^2*by^2 - 2*a^2*by*y1 - a^2*r1^2 + a^2*y1^2 + 2*a*bx*by*y1 + 2*a*bx*r1^2 - 2*a*bx*y1^2 - 2*a*by^2*x1 + 2*a*by*x1*y1 - bx^2*r1^2 + bx^2*y1^2 - 2*bx*by*x1*y1 - by^2*r1^2 + by^2*x1^2, # eq10
by*(a^2*by - 2*a^2*r2 + 2*a*bx*r2 - 2*a*by*x2 + 2*a*r2*x2 - 2*bx*r2*x2 - by*r2^2 + by*x2^2), # eq11
]
end;
(a, b, c) =(arg_a, arg_b, arg_c)
(bx, by) = ( (a^2 - b^2 + c^2)/(2*a), sqrt(-(a - b - c)*(a - b + c)*(a + b - c))*sqrt(a + b + c)/(2*a))
# 求めるパラメータの初期値は,三角形の内接円の半径を勘案して,適当に決める
# 大抵の場合はこれで十分であろう
(R, ax, bx, by) = incenter(a, b, c, ax=true)
iniv = BigFloat[0.74, 1.87, 1.45, 0.63, 2.93, 0.54, 1.03, 1.95, 0.39].*R
res = nls(H, ini=iniv)
vcat(bx, by, res[1])
end;
# driver(507, 375, 252)
描画関数プログラムのソースを見る
function draw(a, b, c, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(bx, by, r1, x1, y1, r2, x2, r3, x3, r4, x4) = driver(a, b, c)
@printf("下斜 = %g; 右斜 = %g; 左斜 = %g; 甲円径 = %.15g; 乙円径 = %.15g; 丙円径 = %.15g; 丁円径 = %.15g\n",
a, b, c, 2r1, 2r2, 2r3, 2r4)
println( (bx, by))
plot([0, a, bx, 0], [0, 0, by, 0], color=:green, lw=0.5)
circle(x1, y1, r1)
circle(x2, r2, r2, :blue)
circle(x3, r3, r3, :magenta)
circle(x4, r4, r4, :orange)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x1, y1, "甲円:r1,(x1,y1)", :red, :center, :bottom, delta=2delta)
point(x2, r2, "乙円:r2\n(x2,r2)", :blue, :center, :bottom, delta=2delta)
point(x3, r3, "丙円:r3\n(x3,r3)", :magenta, :center, :bottom, delta=2delta)
point(x4, r4, "丁円:r4,(x4,r4)", :black, :center, :bottom, delta=2delta)
point(bx, by, "(bx,by)", :green, :center, :bottom, delta=2delta)
point(a, 0, "a", :green, :left, :bottom, delta=2delta)
plot!(xlims=(-10delta, a + 10delta), ylims=(-10delta, by + 5delta))
end
end
draw(350, 289, 231, true)
76.2880204813673
下斜 = 350; 右斜 = 289; 左斜 = 231; 甲円径 = 106.402097379784; 乙円径 = 96.1612747886687; 丙円径 = 81.9018220754186; 丁円径 = 57.5587526228188
(131.9142857142857, 189.6302223393987)
以下のアイコンをクリックして応援してください