算額（その1880） - 算額あれこれ

(二-1) 大阪府池田市住吉住吉神社文化3年(1806)

近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日初版第一刷，大阪教育図書株式会社，大阪市.
キーワード：円8個，正三角形，斜線
#Julia #SymPy #算額 #和算 #数学

正三角形の中に斜線を二本設け，全円 1 個，甲円 1 個，乙円 2 個，丙円 4 個を容れる。全円の直径が 49 寸のとき，丙円の直径はいかほどか。

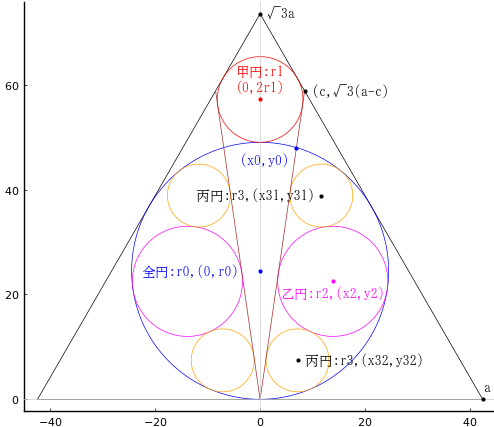
正三角形の一辺の長さを \(2a\)
斜線と斜辺の交点座標を \( (c, (a - c)\sqrt{3})\)
斜線と全円の交点座標を \( (x_0, y_0)\)
全円の半径と中心座標を \(r_0, (0, r_0)\)
甲円の半径と中心座標を \(r_1, (0, 2r_0 + r_1)\)
乙円の半径と中心座標を \(r_2, (x_2, y_2)\)
丙円の半径と中心座標を \(r_3, (x_{31}, y_{31}), (x_{32}, y_{32})\)
とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms r0::positive, r1, r2, a, c, x0, y0
eq6 = (√Sym(3)a - 2r0 - r1) - 2r1
eq7 = (√Sym(3)a - r0) - 2r0
eq8 = dist(c, (a - c)√Sym(3), 0, 0, 0, 2r0 + r1) - r1^2
eq12 = x0^2 + (y0 - r0)^2 - r0^2
eq13 = (a - c)*sqrt(Sym(3))/c - y0/x0
res = solve([eq6, eq7, eq8, eq12, eq13], (a, r1, c, x0, y0))[2] # 2 of 2

(sqrt(3)*r0, r0/3, sqrt(3)*r0/5, 8*sqrt(3)*r0/49, 96*r0/49)

正三角形の一辺の長さは \(2\sqrt{3}\cdot r_0\), 甲円の半径は \(r_0/3\) である。
全円の直径が \(49\) 寸のとき，正三角形の一辺の長さは \(49\sqrt{3} = 84.87048957087498\)，甲円の直径は \(49/3 = 16.333333333333332\) である。

全円により切り取られる斜線は全円の弦である。その長さ \(d\) は以下のようになる。

d = sqrt(res[4]^2 + res[5]^2)#(r0 => 49/2).evalf()

\(\displaystyle \frac{8 \sqrt{3} r_{0}}{7}\)

全円の弦と円弧によりできる領域に 3 個の円（乙円 1 個，丙円 2 個）が入るとき，算法助術の公式29が適用できる。

# d^2 = 16r0*r3 # 算法助術-公式29
r3 = d^2/16r0

\(\displaystyle \frac{12 r_{0}}{49}\)

丙円の半径 \(r_3\) は全円の半径 \(r_0\) の 12/49 倍である。
全円の直径が 49 寸のとき，丙円の直径は 12 寸である。答，術と共に一致する。

また，乙円の半径を \(r_2\) とすると，\(\sqrt{r_0^2 - (d/2)^2} = r_0 - 2r_2\) が成り立つ。

eq14 = sqrt(r0^2 - (d/2)^2) - (r0 - 2r2)

\(\displaystyle - \frac{6 r_{0}}{7} + 2 r_{2}\)

eq14 を解いて，\(r_2 = 3r_0/7\) が得られる。
全円の直径が 49 寸のとき，乙円の直径は 21 寸である。

ans_r2 = solve(eq14, r2)[1] |> factor
ans_r2 |> display

\(\displaystyle \frac{3 r_{0}}{7}\)

ans_r2(r0 => 49/2)

\(\displaystyle 10.5\)

まとめると，全円の直径 \(r_0 = 49\) のとき，正三角形の一辺の長さ \(2a = 49\sqrt{3} ≒ 84.8705\); 甲円の直径 \(r_1 = 49/3 ≒ 16.3333\); 乙円の直径 \(r_2 = 21\); 丙円の直径 \(r_3 = 12\) である。

以下では，図を描くために \(a, r_1, r_2, r_3, c\) と共に，他のパラメータの数値解を求める。

using SymPy
@syms r0, r1, r2, x2, y2, r3, x31, y31, x32, y32, a, c

eq1 = x2^2 + (r0 - y2)^2 - (r0 - r2)^2
eq2 = x31^2 + (r0 - y31)^2 - (r0 - r3)^2
eq3 = x32^2 + (r0 - y32)^2 - (r0 - r3)^2
eq4 = (x2 - x31)^2 + (y2 - y31)^2 - (r2 + r3)^2
eq5 = (x2 - x32)^2 + (y2 - y32)^2 - (r2 + r3)^2
eq6 = (√Sym(3)a - 2r0 - r1) - 2r1
eq7 = (√Sym(3)a - r0) - 2r0
eq8 = dist(c, (a - c)√Sym(3), 0, 0, 0, 2r0 + r1) - r1^2
eq9 = dist(c, (a - c)√Sym(3), 0, 0, x31, y31) - r3^2
eq10 = dist(c, (a - c)√Sym(3), 0, 0, x32, y32) - r3^2
eq11 = dist(c, (a - c)√Sym(3), 0, 0, x2, y2) - r2^2;

function H(u)
(r1, a, c, r2, x2, y2, r3, x31, y31, x32, y32) = u
return [
x2^2 + (r0 - y2)^2 - (r0 - r2)^2, # eq1
x31^2 + (r0 - y31)^2 - (r0 - r3)^2, # eq2
x32^2 + (r0 - y32)^2 - (r0 - r3)^2, # eq3
(x2 - x31)^2 + (y2 - y31)^2 - (r2 + r3)^2, # eq4
(x2 - x32)^2 + (y2 - y32)^2 - (r2 + r3)^2, # eq5
(√3a - 2r0 - r1) - 2r1, # eq6
(√3a - r0) - 2r0, # eq7
dist(c, (a - c)√3, 0, 0, 0, 2r0 + r1) - r1^2, # eq8
dist(c, (a - c)√3, 0, 0, x31, y31) - r3^2, # eq9
dist(c, (a - c)√3, 0, 0, x32, y32) - r3^2, # eq10
dist(c, (a - c)√3, 0, 0, x2, y2) - r2^2 # eq11
]
end;

r0 = 1
iniv = BigFloat[8.1, 42.4, 8.4, 10.5, 13.8, 22.5,
6.0, 11.6, 38.8, 7.2, 7.4]./(49/2)
res = nls(H, ini=iniv)

([0.3333333333333333, 1.7320508075688774, 0.34641016151377546, 0.42857142857142855, 0.5655676106347355, 0.9183673469387755, 0.24489795918367346, 0.4763407495860343, 1.585899805708106, 0.29121529341824953, 0.3033130222802323], true)

\(r_0 = 1\) のとき，\(r_3 = 0.24489795918367346 = r_0\cdot (12/49)\) である。

rationalize(0.24489795918367346)

12//49

描画関数プログラムのソースを見る

function draw(r0, more=true)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, a, c, r2, x2, y2, r3, x31, y31, x32, y32) =
r0 .* [0.3333333333333333, 1.7320508075688774, 0.34641016151377546,
0.42857142857142855, 0.5655676106347355, 0.9183673469387755,
0.24489795918367346, 0.4763407495860343, 1.585899805708106,
0.29121529341824953, 0.3033130222802323]
(x0, y0) = r0/49 .*[8√3, 96]
println("r1 = r0 * ", rationalize(0.3333333333333333, tol=1e-5))
println("r2 = r0 * ", rationalize(0.42857142857142855, tol=1e-5))
println("r3 = r0 * ", rationalize(0.24489795918367346, tol=1e-5))
@printf("全円の直径 = %g; 正三角形の一辺の長さ = %g; 甲円の直径 = %g; 乙円の直径 = %g; 丙円の直径 = %g\n", 2r0, 2√3r0, 2r1, 2r2, 2r3)
plot([a, 0, -a, a], [0, √3a, 0, 0], color=:black, lw=0.5)
circle(0, r0, r0, :blue)
circle(0, 2r0 + r1, r1)
circle2(x2, y2, r2, :magenta)
circle2(x31, y31, r3, :orange)
circle2(x32, y32, r3, :orange)
segment(0, 0, c, (a - c)*sqrt(3), :brown)
segment(0, 0, -c, (a - c)*sqrt(3), :brown)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, r0, "全円:r0,(0,r0)", :blue, :right, :vcenter, deltax=-4delta)
point(0, 2r0 + r1, "甲円:r1\n(0,2r1)", :red, :center, :bottom, delta=delta)
point(x2, y2, "乙円:r2,(x2,y2)", :magenta, :center, delta=-delta)
point(x31, y31, "丙円:r3,(x31,y31) ", :black, :right, :vcenter)
point(x32, y32, " 丙円:r3,(x32,y32)", :black, :left, :vcenter)
point(a, 0, "a", :black, :left, :bottom, delta=delta)
point(0, √3a, " √3a", :black, :left, :vcenter)
point(x0, y0, "(x0,y0) ", :blue, :right, delta=-delta)
point(c, √3(a - c), " (c,√3(a-c)", :black, :left, :vcenter)
end
end;