算額（その1492） - 算額あれこれ

12 岩手県胆沢町若柳市野々個人宅安政2年(1855)

安富有恒：和算—岩手の現存算額のすべて，青磁社，東京都，1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf
キーワード：円5個，外円，弦，斜線
#Julia #SymPy #算額 #和算 #数学

外円の中に弦と斜線を描き，隙間に等円 4 個を容れる。等円と弦，斜線に囲まれた部分の面積を求めよ。

注：等円は外円に内接し，弦，斜線に外接する。

図形自体は「算額（その725）」と同じであり，円と弦に囲まれた部分の面積を求めよということである。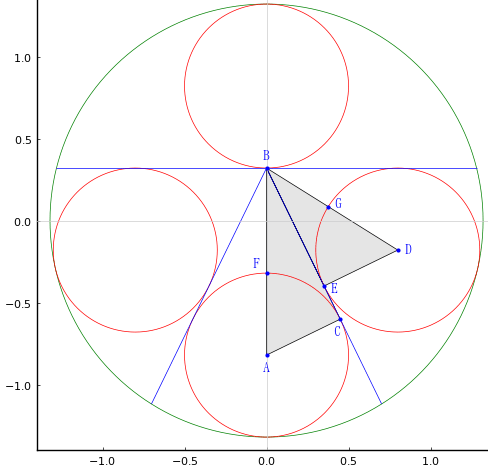

外円の半径と中心座標を \(R, (0, 0)\)
等円の半径と中心座標を \(r, (x, R - 3r), (0, r - R), (0, R - r)\)
斜線と外円の交点座標を \( (x_0, y_0)\)
とおき，\(R, x, x_0, y_0\) を未知数として以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms R::positive, r::positive, x::positive, x0::positive, y0::negative
eq1 = x^2 + (R - 3r)^2 - (R - r)^2
eq2 = x0^2 + y0^2 - R^2
eq3 = x0/sqrt(x0^2 + (R - 2r - y0)^2) - r/(2R - 2r)
eq3 = dist2(0, R - 2r, x0, y0, x, R - 3r, r)
eq4 = dist2(0, R - 2r, x0, y0, 0, r - R, r)
res = solve([eq1, eq2, eq3, eq4], (R, x, x0, y0))[1]

(r*(sqrt(17) + 17)/8, r*sqrt(-4 + sqrt(17))*(sqrt(17) + 5)/2, 4*r*sqrt(-4 + sqrt(17)), r*(-55 + 9*sqrt(17))/8)

黒積は，直角三角形の面積から扇型の面積を差し引いたもので表すことができる。
等円の直径が 1 なので，\(r = AC = DE = 1/2\)
外円の半径が \(R = r(\sqrt{17} + 17)/8\) なので
\(AB = 2R - 3r\)
\(x = r\sqrt{\sqrt{17} - 4}\cdot (\sqrt{17} + 5)/2\)
\(DB = \sqrt{x^2 + r^2}\)
\(∠BAC = \text{acos}(r/AB)\)
\(∠BDE = \text{acos}(r/DB)\)
\(⊿ABC = AB\sin(∠BAC)r/2\)
\(⊿DBA = x r/2\)
\(面積 = 2( (⊿ABC - \pi r^2 (∠BAC/2\pi)) + 2(⊿DBA - \pi r^2(∠BDE/2\pi)))\)
等円の直径が 1.0 のとき，黒積は 0.5273103412996156 である。

描画関数プログラムのソースを見る

function draw(r, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(R, x, x0, y0) = (r*(sqrt(17) + 17)/8, r*sqrt(-4 + sqrt(17))*(sqrt(17) + 5)/2, 4*r*sqrt(-4 + sqrt(17)), r*(-55 + 9*sqrt(17))/8)
y00 = R - 2r
x00 = sqrt(R^2 - y00^2)
(x01, y01) = foot(0, R - 2r, x0, y0, 0, r - R)
(x02, y02) = foot(0, R - 2r, x0, y0, x, R - 3r)
plot([0, 0, x01, 0, x,x02, 0], [y00, r - R, y01, y00, R - 3r, y02, y00], color=:gray90, seriestype=:shape, fillcolor=:gray90, lw=0.5)
circle(0, 0, R, :green)
circle2(x, R - 3r, r)
circle22(0, r - R, r)
segment(-x00, y00, x00, y00, :blue)
plot!([-x0, 0, x0], [y0, y00, y0], color=:blue, lw=0.5)
# 黒積の計算
AB = 2R - 3r
∠BAC = acos(r/AB)
BD = sqrt(x^2 + r^2)
∠BDE = acos(r/BD)
⊿ABC = AB*sin(∠BAC)*r/2
⊿DBE = x*r/2
黒積 = 2*( (⊿ABC - π*r^2*(∠BAC/2π)) + 2(⊿DBE - π*r^2*(∠BDE/2π)))
@printf("等円の直径が %g のとき，黒積は %g である。", 2r, 黒積)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, r - R, "A", :blue, :center, delta=-delta)
point(0, y00, "B", :blue, :center, :bottom, delta=delta)
point(x01, y01, "C", :blue, :right, delta=-delta)
point(x, R - 3r, " D", :blue, :left, :vcenter)
point(x02, y02, " E", :blue, :left, :vcenter, delta=-delta/2)
point(0, 2r - R, "F ", :blue, :right, :bottom, delta=delta/2)
point( (BD - r)*sin(∠BDE), y00 - (BD - r)*cos(∠BDE), " G", :blue, :left, :vcenter, delta=delta/2)
end
end;