算額（その814） - 算額あれこれ

藤田貞資：精要算法（下巻）天明元年(1781)

http://www.wasan.jp/seiyou/seiyou.html
キーワード：円6個，正五角形
#Julia #SymPy #算額 #和算 #数学

外円内に 5 個の等円を容れる。外円と等円に挟まれる部分の面積（黒積）が 2330.89 歩のとき，等円の直径を求めよ。

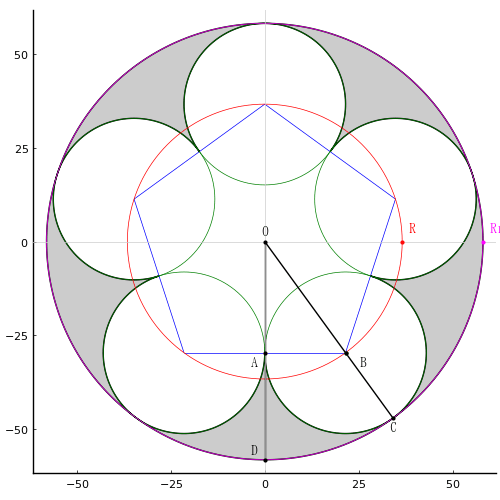
黒積は，「扇形 OCD - 直角三角形 OAB - 扇形ACB」の面積の 10 倍である。
等円の半径 OB = R，AB = r とすれば，∠AOB = 36° より，R = r/sind(36)
OC = OB + BC = R + r = Rr とすれば，
扇形 OCD = πRr^2/10
直角三角形 OAB = r*R*cosd(36)/2
扇形 ACB = πr^2*(126/360)
よって，黒積 = 10*(π*Rr^2/10 - r*R*cosd(36)/2 - π*r^2*126/360)
黒積 = 2332.89 を解いて r を求めると，r = 21.5000025771553，等円の直径は 43.0000051543107 寸である。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms r::positive, R::positive, Rr::positive,
黒積::positive, BLK::positive

R = solve(R*sind(Sym(36)) - r, R)[1]
Rr = R + r
R |> println
Rr |> println
(R.evalf(), Rr.evalf()) |> println

2*sqrt(2)*r/sqrt(5 - sqrt(5))
r + 2*sqrt(2)*r/sqrt(5 - sqrt(5))
(1.70130161670408*r, 2.70130161670408*r)

黒積 = PI*Rr^2/10 - R*r*cosd(Sym(36))/2 - PI*r^2*126//360
eq = 10黒積 - BLK # 2332.89;
eq |> println

-BLK - 7*pi*r^2/2 - 10*sqrt(2)*r^2*(1/4 + sqrt(5)/4)/sqrt(5 - sqrt(5)) + pi*(r + 2*sqrt(2)*r/sqrt(5 - sqrt(5)))^2

方程式を解いて，等円の直径を求める。

res = 2solve(eq, r)[1]
res |> println

2*sqrt(2)*sqrt(BLK)*(5 - sqrt(5))^(3/4)/sqrt(-8*sqrt(10)*pi - 20*sqrt(10) - 9*pi*sqrt(5 - sqrt(5)) + 5*sqrt(5)*pi*sqrt(5 - sqrt(5)) + 40*sqrt(2)*pi)

黒積が 2332.89 のときの等円の直径を求める。

res(BLK => 2332.89) |> println

96.6*sqrt(2)*(5 - sqrt(5))^(3/4)/sqrt(-8*sqrt(10)*pi - 20*sqrt(10) - 9*pi*sqrt(5 - sqrt(5)) + 5*sqrt(5)*pi*sqrt(5 - sqrt(5)) + 40*sqrt(2)*pi)

等円の直径は 43 寸である。

res(BLK => 2332.89).evalf() |> println

43.0000051543107

描画関数プログラムのソースを見る

function transform(x, y; deg=0, dx=0, dy=0)
return [cosd(deg) -sind(deg); sind(deg) cosd(deg)] * [x, y]
end;

function rotatefigure(x2, y2)
for i in 1:5
plot!(x2, y2, color=:gray80, seriestype=:shape, fillcolor=:gray80)
i == 5 && return
(x2, y2) = transform(x2, y2, deg = 72)
end
end;

function fillblack(r, Rr, x, y)
x2 =
y2 =
for i in 180:0.5:306
append!(x2, r*cosd(i) + x[1])
append!(y2, r*sind(i) + y[1])
end
for i in 306:-0.5:270
append!(x2, Rr*cosd(i))
append!(y2, Rr*sind(i))
end
x2 = vcat(x2, -reverse(x2))
y2 = vcat(y2, reverse(y2))
rotatefigure(x2, y2)
end;

function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
x = Vector{Float64}(undef, 6)
y = Vector{Float64}(undef, 6)
r = 21.5000025771553
R = 2√2*r/sqrt(5 - √5)
Rr = R + r
blk = 10(π*Rr^2/10 - R*r*cosd(36)/2 - π*r^2*126/360)
@printf("等円の直径 = %g; 黒積 = %g; R = %g; Rr = %g\n", 2r, blk, R, Rr)
for i = 1:6
θ = 306 + (i - 1)*72
x[i] = R*cosd(θ)
y[i] = R*sind(θ)
end
plot()
fillblack(r, Rr, x, y)
for i = 1:5
segment(x[i], y[i], x[i + 1], y[i + 1], :blue)
circle(x[i], y[i], r, :green)
end
circle(0, 0, R)
circle(0, 0, Rr, :magenta)
segment(0, 0, 0, -Rr, :black, lw=1)
segment(0, 0, Rr*cosd(306), Rr*sind(306), :black, lw=1)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x[1], y[1])
point(R, 0, " R", :red, :left, :bottom, delta=delta)
point(Rr, 0, " Rr", :magenta, :left, :bottom, delta=delta)
point(0, -R*cosd(36), "A ", :black, :right, delta=-delta/2)
point(x[1], y[1], " B", :black, :left, delta=-delta/2)
point(Rr*cosd(306), Rr*sind(306), "C", :black, :center, delta=-delta/2)
point(0, -Rr, "D ", :black, :right, :bottom, delta=delta/2)
point(0, 0, "O", :black, :center, :bottom, delta=delta/2)
end
end;