算額（その720） - 算額あれこれ

長野県諏訪市中洲諏訪大明神社天保12年(1841)

中村信弥「改訂増補長野県の算額」県内の算額(P.153)
http://www.wasan.jp/zoho/zoho.html
キーワード：円3個，正五角形，対角線
#Julia #SymPy #算額 #和算 #数学

正五角形に 2 本の対角線を引き，区画された領域に大円，中円，小円，正方形を容れる。対角線の長さの 8 乗が 256 となるときの，それぞれの大きさはいかほどか。

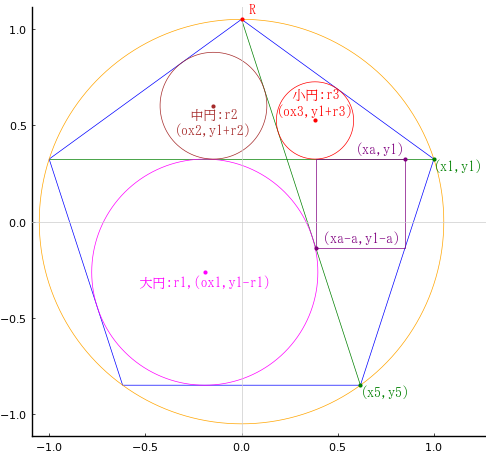
正五角形が内接する円の直径を \(R\) として 5 個の頂点の座標を以下のように定義する。
対角線の長さが \(2x_1 = 2\) なので，条件が成り立つときの \(R\) は \(2x_1 = R \cos(2\pi/20) = 2\) より，\(R = 1/\cos(\pi/10)=\sec(\pi/10)\) である。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms R::positive, r1, ox1::negative, r2, ox2::negative, r3, ox3, xa, a
R = sec(PI/10)
(x1, y1) = R.*(cos(2PI/20), sin(2PI/20))
(x2, y2) = (0, R)
(x3, y3) = (-x1, y1)
(x4, y4) = R.*(-sin(2PI/10), -cos(2PI/10))
(x5, y5) = (-x4, y4);

以下の連立方程式を解く。

eq1 = (y1 - y4)/2 - r1
eq2 = (x3 + x5)/2 - ox1;

eq3 = dist2(x2, y2, x3, y3, ox2, y1 + r2, r2)
eq4 = dist2(x2, y2, x5, y5, ox2, y1 + r2, r2)

eq5 = dist2(x2, y2, x5, y5, ox3, y1 + r3, r3)
eq6 = dist2(x2, y2, x1, y1, ox3, y1 + r3, r3)

eq7 = (x1 - xa)*(y1 - y5) - (x1 - x5)*a
eq8 = (x5 - xa + a)*(y2 - y5) - x5*(y1 - a - y5);

res = solve([eq1, eq2,eq3, eq4, eq5, eq6, eq7, eq8], (r1, ox1, r2, ox2, r3, ox3, xa, a))[11]; # 11 of 12

# r1
@show(res[1] |> factor)

res[1] |> factor = (-sqrt(2) + sqrt(10))*sqrt(sqrt(5) + 5)/8

\(\displaystyle \frac{\left(- \sqrt{2} + \sqrt{10}\right) \sqrt{\sqrt{5} + 5}}{8}\)

res[1].evalf() * 2

\(\displaystyle 1.17557050458495\)

# ox1
@show(res[2] |> factor)

res[2] |> factor = (-3 + sqrt(5))/4

\(\displaystyle \frac{-3 + \sqrt{5}}{4}\)

# r2
@show(res[3] |> factor |> sympy.sqrtdenest |> factor)

( (res[3] |> factor) |> sympy.sqrtdenest) |> factor = -(-7*sqrt(2) + 3*sqrt(10))*sqrt(sqrt(5) + 5)/4

\(\displaystyle - \frac{\left(- 7 \sqrt{2} + 3 \sqrt{10}\right) \sqrt{\sqrt{5} + 5}}{4}\)

res[3].evalf() * 2

\(\displaystyle 0.555029102851551\)

# ox2
@show(res[4] |> factor)

res[4] |> factor = (-3 + 2*sqrt(9 - 4*sqrt(5)) + sqrt(5))/2

\(\displaystyle \frac{-3 + 2 \sqrt{9 - 4 \sqrt{5}} + \sqrt{5}}{2}\)

res[4] |> factor |> simplify

\(\displaystyle - \frac{3}{2} + \sqrt{9 - 4 \sqrt{5}} + \frac{\sqrt{5}}{2}\)

# r3
@show(res[5] |> factor |> sympy.sqrtdenest |> factor)

( (res[5] |> factor) |> sympy.sqrtdenest) |> factor = -(-5*sqrt(2) + 2*sqrt(10))*sqrt(sqrt(5) + 5)/10

\(\displaystyle - \frac{\left(- 5 \sqrt{2} + 2 \sqrt{10}\right) \sqrt{\sqrt{5} + 5}}{10}\)

res[5].evalf() * 2

\(\displaystyle 0.401622831772455\)

# ox3
@show(res[6] |> sympy.sqrtdenest |> factor)

(res[6] |> sympy.sqrtdenest) |> factor = -(-3 + sqrt(5))/2

\(\displaystyle - \frac{-3 + \sqrt{5}}{2}\)

# xa
@show(res[7] |> factor)

res[7] |> factor = (-11*sqrt(2)*sqrt(sqrt(5) + 5) - 14 + 3*sqrt(10)*sqrt(sqrt(5) + 5) + 28*sqrt(5))/38

\(\displaystyle \frac{- 11 \sqrt{2} \sqrt{\sqrt{5} + 5} - 14 + 3 \sqrt{10} \sqrt{\sqrt{5} + 5} + 28 \sqrt{5}}{38}\)

# a
@show(res[8] |> factor)

res[8] |> factor = (-11*sqrt(2)*sqrt(sqrt(5) + 5) + 5 + 9*sqrt(5) + 3*sqrt(10)*sqrt(sqrt(5) + 5))/19

\(\displaystyle \frac{- 11 \sqrt{2} \sqrt{\sqrt{5} + 5} + 5 + 9 \sqrt{5} + 3 \sqrt{10} \sqrt{\sqrt{5} + 5}}{19}\)

res[8].evalf()

\(\displaystyle 0.463034175319608\)

大円の直径 = 1.17557050458495
中円の直径 = 0.555029102851551
小円の直径 = 0.401622831772455
正方形の一辺の長さ = 0.463034175319608

描画関数プログラムのソースを見る

function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
R = sec(pi/10)
(x1, y1) = R.*(cos(2pi/20), sin(2pi/20))
(x2, y2) = (0, R)
(x3, y3) = (-x1, y1)
(x4, y4) = R.*(-sin(2pi/10), -cos(2pi/10))
(x5, y5) = (-x4, y4)
t = sqrt(√5 + 5)
r1 = (√10 - √2)*t/8
ox1 = (√5 - 3)/4
r2 = (7√2 - 3√10)*t/4
ox2 = (2sqrt(9 - 4√5) + √5 - 3)/2
r3 = (5√2 - 2√10)*t/10
ox3 = (3 - √5)/2
xa = (28√5 + 3√10t -11√2*t - 14)/38
a = (9√5 + 3√10t -11√2*t + 5)/19
plot([x1, x2, x3, x4, x5, x1], [y1, y2, y3, y4, y5, y1], color=:blue, lw=0.5)
segment(x2, y2, x5, y5, :green)
segment(x1, y1, x3, y3, :green)
circle(0, 0, R, :orange)
circle(ox1, y1 - r1, r1, :magenta)
circle(ox2, y1 + r2, r2, :brown)
circle(ox3, y1 + r3, r3, :red)
rect(xa - a, y1-a, xa, y1, :purple)
println("大円の直径 = ", 2r1)
println("中円の直径 = ", 2r2)
println("小円の直径 = ", 2r3)
println("正方形の一辺の長さ = ", a)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, R, " R", :red, :left, :bottom, delta=delta/2)
point(xa, y1, "(xa,y1)", :purple, :right, :bottom, delta=delta/2)
point(xa - a, y1-a, " (xa-a,y1-a)", :purple, :left, :bottom, delta=delta/2)
point(ox1, y1 - r1, "大円:r1,(ox1,y1-r1)", :magenta, :center, delta=-delta/2)
point(ox2, y1 + r2, "中円:r2\n(ox2,y1+r2)", :brown, :center, delta=-delta/2)
point(ox3, y1 + r3, "小円:r3\n(ox3,y1+r3)", :red, :center, :bottom, delta=delta/2)
point(x1, y1, "(x1,y1)")
point(x5, y5, "(x5,y5)")
end
end;