算額（その662） - 算額あれこれ

茨城県笠間市福原吾國山上頂神（吾国山上頂神前）文化7年(1810)

中村信弥「改訂増補長野県の算額」県外の算額(P.288)
http://www.wasan.jp/zoho/zoho.html
キーワード：菱形，正方形，斜線
#Julia #SymPy #算額 #和算 #数学

長径，短径が 8 寸，6 寸の菱形の中に一辺の長さ 3 寸の正方形と斜線が入っている。斜線の長さはいかほどか。

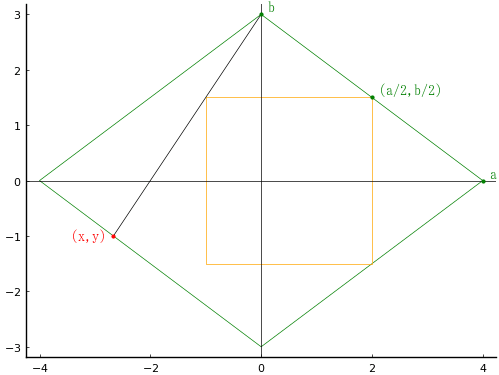
斜線と菱形の辺の交点座標を (x, y) とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms x::negative, y::negative
(a, b) = (Sym(4), Sym(3))
eq1 = (b - y)/(-x) - b//2
eq2 = sqrt( (a + x)^2 + (-y)^2) + sqrt( (-x)^2 + (b + y)^2) - sqrt(a^2 + b^2)
res = solve([eq1, eq2], (x, y))[1]

(-8/3, -1)

(x, y) = (-8/3, -1)
長さは sqrt(x^2 + (b - y)^2) = 4√13/3 = 4.80740170061865，4寸8分あまりである。

(x, y) = res[1]
長さ = sqrt(x^2 + (b - y)^2)
(長さ, 長さ.evalf()) |> println

(4*sqrt(13)/3, 4.80740170061865)

描画関数プログラムのソースを見る

function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(a, b) = (4, 3)
(x, y) = (-8/3, -1)
plot([a, 0, -a, 0, a], [0, b, 0, -b, 0], color=:green, lw=0.5)
plot!([2, -1, -1, 2, 2], [3/2, 3/2, -3/2, -3/2, 3/2], color=:orange, lw=0.5)
segment(0, 3, x, y)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
point(x, y, "(x,y) ", :red, :right, :vcenter)
point(a, 0, " a", :green, :left, :bottom)
point(0, b, " b", :green, :left, :bottom)
point(a/2, b/2, " (a/2,b/", :green, :left, :bottom)
end
end;