算額（その654） - 算額あれこれ

群馬の算額 44-2 八幡宮

http://takasakiwasan.web.fc2.com/gunnsann/g044-2.html
キーワード：円2個，円弧，台形
#Julia #SymPy #算額 #和算 #数学

下底 20 寸，上底 15 寸，高さ 6 寸の台形内に，円弧と等円 2 個を置く。等円の直径を求めよ。

算額の原図を左右反転させ，台形の左下頂点を原点に置き，下底の長さを a，高さを h とする。
台形は等脚台形でなくてもよいので，左上，右上の頂点座標を(b1, h), (b2, h) とおく。
等円の半径と中心座標を r, (x1, r), (x2, h - r)
円弧を構成する円の半径と中心座標を R, (x, y)
とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms a::positive, b1::positive, b2::positive, h::positive,
R::positive, x::positive, y::positive,
r::positive, x1::positive, x2::positive
eq1 = (x - a)^2 + y^2 - R^2
eq2 = (x - b1)^2 + (y - h)^2 - R^2
eq3 = (x - x1)^2 + (y - r)^2 - (R + r)^2
eq4 = (x - x2)^2 + (y - h + r)^2 - (R - r)^2
eq5 = dist(0, 0, b1, h, x1, r) - r^2
eq6 = dist(a, 0, b2, h, x2, h - r) - r^2;

function H(u)
(R, x, y, r, x1, x2) = u
return [
-R^2 + y^2 + (-a + x)^2, # eq1
-R^2 + (-b1 + x)^2 + (-h + y)^2, # eq2
-(R + r)^2 + (-r + y)^2 + (x - x1)^2, # eq3
-(R - r)^2 + (x - x2)^2 + (-h + r + y)^2, # eq4
-r^2 + (-b1*(b1*x1 + h*r)/(b1^2 + h^2) + x1)^2 + (-h*(b1*x1 + h*r)/(b1^2 + h^2) + r)^2, # eq5
-r^2 + (-a + x2 - (-a + b2)*(h*(h - r) + (-a + b2)*(-a + x2))/(h^2 + (-a + b2)^2))^2 + (h - h*(h*(h - r) + (-a + b2)*(-a + x2))/(h^2 + (-a + b2)^2) - r)^2, # eq6
]
end;

(a, b1, b2, h) = (20, 2.5, 17.5, 6)
iniv = BigFloat[58, 30, 57, 2.5, 4, 16]

res = nls(H, ini=iniv)

([57.56982255166218, 29.678706199460915, 56.750393081761004, 2.522911051212938, 3.784366576819407, 15.818059299191376], true)

台形が等脚台形（h = 6; a = 20; b1 = 2.5; b2 = 17.5）の場合，R = 57.5698; x = 29.6787; y = 56.7504; r = 2.52291; x1 = 3.78437; x2 = 15.8181
となり，等円の直径は約 5.04582 である。

なお，台形は等脚台形でなくても構わない（条件の範囲内で）。
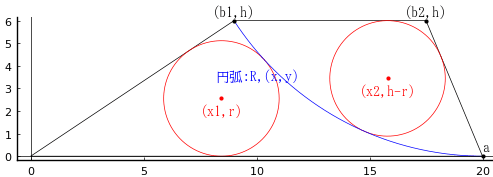
たとえば，下図のような場合，パラメータは以下の通りである。

\(h = 6; a = 20; b_1 = 9; b_2 = 17.5; R = 13.1643\)
\(x = 20.0441; y = 13.1643; r = 2.55614; x_1 = 8.44236; x_2 = 15.7959\)

描画関数プログラムのソースを見る

function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(R, x, y, r, x1, x2) = res[1]
@printf("h = %g; a = %g; b1 = %g; b2 = %g; R = %g; x = %g; y = %g; r = %g; x1 = %g; x2 = %g\n", h, a, b1, b2, R, x, y, r, x1, x2)
plot([0, a, b2, b1, 0], [0, 0, h, h, 0], color=:black, lw=0.5)
circle(x1, r, r)
circle(x2, h - r, r)
θ1 = atand( (y - h)/(x - b1))
θ2 = atand(y/(x - a))
circle(x, y, R, :blue, beginangle=180 + θ1, endangle=180 + θ2, by=0.05)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
point(x1, r, "(x1,r)", :red, :center, delta=-3delta)
point(x2, h - r, "(x2,h-r)", :red, :center, delta=-3delta)
point(b1, h, "(b1,h)", :black, :center, :bottom, delta=delta)
point(b2, h, "(b2,h)", :black, :center, :bottom, delta=delta)
point(a, 0, " a", :black, :center, :bottom, delta=delta)
point(a/2, h/2, "円弧:R,(x,y)", :blue, :center, :bottom, delta=3delta, mark=false)
end
end;