算額（その643） - 算額あれこれ

長野県軽井沢町峠熊野神社安政4年(1857)

中村信弥「改訂増補長野県の算額」県内の算額(P.201)
http://www.wasan.jp/zoho/zoho.html
キーワード：円3個，外円，円弧
#Julia #SymPy #算額 #和算 #数学

外円の中に 4 つの円弧と 2 つの等円が入っている。等円は互いに外接し円弧とも外接している。
大矢，小矢がそれぞれ 49寸，36.75寸のとき，等円の直径を求めよ。

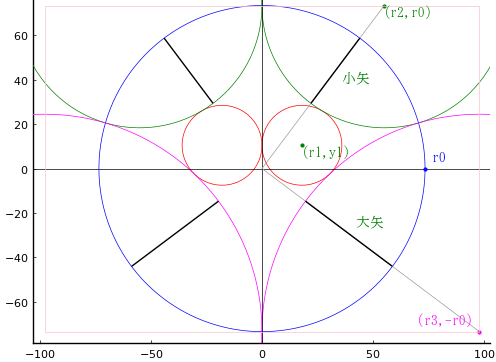
外円の半径と中心座標を \(r_0,\ (0,\ 0)\)
等円の半径と中心座標を \(r_1,\ (r_1,\ y_1)\)
上部の円弧を構成する円の半径と中心座標を \(r_2,\ (r_2,\ r_0)\)
下部の円弧を構成する円の半径と中心座標を \(r_3,\ (r_3,\ -r_0)\)
とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms r0::positive, r1::positive, y1::positive, r2::positive, r3::positive

eq1 = (r2 - r1)^2 + (r0 - y1)^2 - (r1 + r2)^2
eq2 = r2^2 + r0^2 - (r0 + r2 - 3675//100)^2
eq3 = r3^2 + r0^2 - (r0 + r3 - 49)^2
eq4 = r0 - sqrt(r2*r3)
eq5 = 1/sqrt(r2) + 1/sqrt(r3) - 1/sqrt(r1);

function H(u)
(r0, r1, y1, r2, r3) = u
return [
(r0 - y1)^2 + (-r1 + r2)^2 - (r1 + r2)^2, # eq1
r0^2 + r2^2 - (r0 + r2 - 147/4)^2, # eq2
r0^2 + r3^2 - (r0 + r3 - 49)^2, # eq3
r0 - sqrt(r2)*sqrt(r3), # eq4
1/sqrt(r3) + 1/sqrt(r2) - 1/sqrt(r1), # eq5
]
end;

iniv = BigFloat[73.5, 20, 10, 54, 97]
res = nls(H, ini=iniv)

(BigFloat[73.5, 18.0, 10.5, 55.125, 98.0], true)

等円の半径は 18 寸である（直径 36寸）。
その他のパラメータは以下の通りである。

\(r_0 = 73.5; r_1 = 18; y_1 = 10.5; r_2 = 55.125; r_3 = 98\)

描画関数プログラムのソースを見る

function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r0, r1, y1, r2, r3) = res[1]
@printf("r0 = %g; r1 = %g; y1 = %g; r2 = %g; r3 = %g\n", r0, r1, y1, r2, r3)
plot()
circle(0, 0, r0, :blue)
circle(r1, y1, r1)
circle(-r1, y1, r1)
circle(r2, r0, r2, :green)
circle(-r2, r0, r2, :green)
circle(r3, -r0, r3, :magenta)
circle(-r3, -r0, r3, :magenta)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
point(r1, y1, "(r1,y1)",)
point(r2, r0, "(r2,r0)")
point(r3, -r0, "(r3,-r0) ", :magenta, :right, :bottom, delta=delta/2)
point(r0, 0, " r0", :blue, :left, :bottom, delta=delta/2)
fr3 = Float64(r3)
fr0 = Float64(r0)
rect(-fr3, -fr0, fr3, fr0)
plot!(xlims=(-fr3 - 5, fr3 + 5), ylims=(-fr0 - 5, fr0 + 5))
θ = atand(r0/r2)
(px1, py1, px2, py2) = (r0*cosd(θ), r0*sind(θ), 2(r0 - r2)*cosd(θ), 2(r0 - r2)*sind(θ))
segment(0, 0, r2, r0, :gray60)
segment(px1, py1, px2, py2, lw=1)
segment(-px1, py1, -px2, py2, lw=1)
point( (px1 + px2)/2, (py1 + py2)/2, " 小矢", mark=false)
θ = atand(-r0/r3)
(px1, py1, px2, py2) = (r0*cosd(θ), r0*sind(θ), -(r0 - r3)*cosd(θ), -(r0 - r3)*sind(θ))
segment(0, 0, r3, -r0, :gray60)
segment(px1, py1, px2, py2, lw=1)
segment(-px1, py1, -px2, py2, lw=1)
point( (px1 + px2)/2, (py1 + py2)/2, " 大矢", mark=false, delta=2delta)
end
end;