算額（その438） - 算額あれこれ

奥州堺社天明2年(1782)

下野国那須郡須賀川邑社丈右衛門正常
藤田貞資(1789)：神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf
キーワード：円17個
#Julia #SymPy #算額 #和算 #数学

交差する 2 個の大円の中に，等円 3 個，甲円，乙円，丙円がそれぞれ 4 個ずつ入っている。大円の直径が与えられたとき，大円の直径が与えられたとき，各円の直径を求めよ。

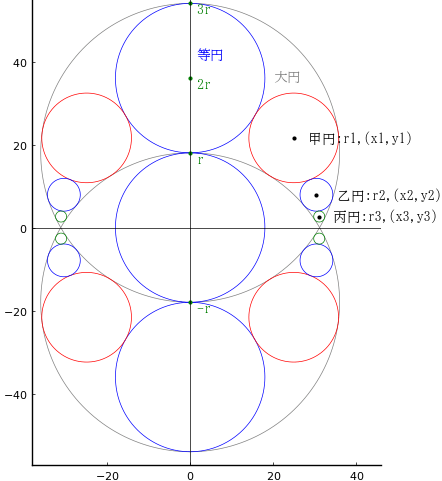
大円の半径と中心座標を \(2r,\ (0,\ r),\ (0,\ -r)\)
等円の半径と中心座標を \(r,\ (0,\ 2r),\ (0,\ 0),\ (0,\ -2r)\)
甲円の半径と中心座標を \(r_1,\ (x_1,\ y_1)\)
乙円の半径と中心座標を \(r_2,\ (x_2,\ y_2)\)
丙円の半径と中心座標を \(r_3,\ (x_3,\ y_3)\)
として以下の連立方程式の解を求める。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms r0::positive, r::positive,
r1::positive, x1::positive, y1::positive,
r2::positive, x2::positive, y2::positive,
r3::positive, x3::positive, y3::positive,
r4::positive, x4::positive, y4::positive,
r5::positive, x5::positive, y5::positive,
r6::positive, x6::positive, y6::positive;

r = r0//2
eq1 = x1^2 + (y1 + r)^2 - (2r + r1)^2
eq2 = x1^2 + (y1 - r)^2 - (2r - r1)^2
eq3 = x1^2 + (2r - y1)^2 - (r1 + r)^2

eq4 = (x1 - x2)^2 + (y1 - y2)^2 - (r1 + r2)^2
eq5 = x2^2 + (r - y2)^2 - (2r - r2)^2
eq6 = x2^2 + (y2 + r)^2 - (2r + r2)^2

eq7 = x3^2 + (r - y3)^2 - (2r - r3)^2
eq8 = (x2 - x3)^2 + (y2 - y3)^2 - (r2 + r3)^2
eq9 = x3^2 + (y3 + r)^2 - (2r + r3)^2;

solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9], (r1, x1, y1, r2, x2, y2, r3, x3, y3))[1] # 1 of 2

(3*r0/10, 2*sqrt(3)*r0/5, 3*r0/5, 9*r0/82, 20*sqrt(3)*r0/41, 9*r0/41, 27*r0/730, 182*sqrt(3)*r0/365, 27*r0/365)

\(r_0 = 36;\ r = 18;\ r_1 = 10.8;\ x_1 = 24.9415;\ y_1 = 21.6\)
\(r_2 = 3.95122;\ x_2 = 30.4165;\ y_2 = 7.90244\)
\(r_3 = 1.33151;\ x_3 = 31.0915;\ y_3 = 2.66301\)

円の直径だけをいえば，甲円，乙円，丙円の直径は大円の直径のそれぞれ 3/10, 9/82, 27/730 倍である。

\(大円の直径 = 72\ のとき，等円の直径 = 36;\ 甲円の直径 = 21.6\)
\(乙円の直径 = 7.90244;\ 丙円の直径 = 2.66301\)

72 .* [3/10, 9/82, 27/730] |> println

[21.599999999999998, 7.902439024390244, 2.663013698630137]

描画関数プログラムのソースを見る

function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r0 = 72/2
r = r0/2
(r1, x1, y1, r2, x2, y2, r3, x3, y3) = (3*r0/10, 2*sqrt(3)*r0/5, 3*r0/5, 9*r0/82, 20*sqrt(3)*r0/41, 9*r0/41, 27*r0/730, 182*sqrt(3)*r0/365, 27*r0/365)
@printf("r0 = %g; r = %g; r1 = %g; x1 = %g; y1 = %g; r2 = %g; x2 = %g; y2 = %g; r3 = %g; x3 = %g; y3 = %g\n",
r0, r, r1, x1, y1, r2, x2, y2, r3, x3, y3)
@printf("大円の直径 = %g; 等円の直径 = %g; 甲円の直径 = %g; 乙円の直径 = %g; 丙円の直径 = %g\n", 2r0, 2r, 2r1, 2r2, 2r3)
plot()
circle(0, r, r0, :gray)
circle(0, -r, r0, :gray)
circle(0, 2r, r, :blue)
circle(0, -2r, r, :blue)
circle(0, 0, r, :blue)
circle4(x1, y1, r1)
circle4(x2, y2, r2, :blue)
circle4(x3, y3, r3, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) / 3 # size[2] * fontsize * 2
point(x1, y1, " 甲円:r1,(x1,y1)", :black, :left, :vcenter)
point(x2, y2, " 乙円:r2,(x2,y2)", :black, :left, :vcenter)
point(x3, y3, " 丙円:r3,(x3,y3)", :black, :left, :vcenter)
point(0, r, " r")
point(0, -r, " -r")
point(0, 2r, " 2r")
point(0, 3r, " 3r")
point(0.08r, 2.4r, "等円", :blue, mark=false)
point(0.8x1, 2.1r, "大円", :gray, mark=false)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
end
end;