算額（その177） - 算額あれこれ

愛媛県四国中央市川之江町八幡神社平成21年(2009)

川之江高等学校の和算勉強会が奉納した「算額(大円内等円発展題)」平成21年
https://www.fureai-cloud.jp/tie/doc/view/10455/
キーワード：円環，外円
#Julia #SymPy #算額 #和算 #数学

径が 1 寸の外円の中に，等円を 3 個容れる場合，等円の径を求めよ。さらに，5 個，8 個を容れる場合も求めよ。

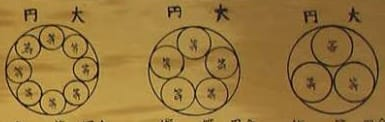
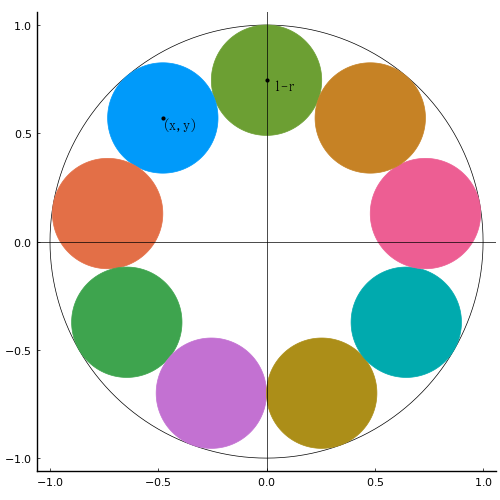
外円の半径を 1 とし，その中に半径 \(r\) の \(n\) 個の等円を入れることを考える(\(n ≧ 2\))。
時計盤でいえば12時の位置にある等円と，それに対して反時計回りで左隣にある等円を考える。
隣り合う円が外接するという方程式を解き等円の半径を求めることができる。

以下は，\(n\) を与えて \(r\)（数式と数値）を求める関数である。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms r::positive, x, y

function getradius(n=3)
θ = 2PI / n + PI / 2
x = (1 - r)cos(θ)
y = (1 - r)sin(θ)
eq = x^2 + (1 - r - y)^2 - 4r^2 # 隣り合う等円が外接する
res = solve(eq)[1]
simplify(res), float(res.evalf())
end;

実際に求めてみる。
等円を 3 個入れる場合

getradius(3)

(-3 + 2*sqrt(3), 0.464101615137755)

術曰　3の平方根を2倍し3を引く
答曰　4分6厘4毛1糸あまりあり

等円を 5 個入れる場合

getradius(5)

(-5 - sqrt(50 - 10*sqrt(5))/2 + 3*sqrt(10 - 2*sqrt(5))/2 + 2*sqrt(5), 0.370191908158750)

等円を 8 個入れる場合

getradius(8)

(-3 - sqrt(4 - 2*sqrt(2)) + 2*sqrt(2 - sqrt(2)) + 2*sqrt(2), 0.276768653914155)

描画関数プログラムのソースを見る

function draw(n, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
expression, r = getradius(n)
@printf("r = %s\n = %g\n", expression, r)
plot()
circle(0, 0, 1, :black)
for i = 0:n-1
θ = 2pi/n*i + pi/2
(x, y) = (1 - r) .* (cos(θ), sin(θ))
circle(x, y, r, i, fill=true)
if more && i == 1
point(0, 1 - r, " 1-r", :black)
point(x, y, "(x,y)", :black)
end
end
if more
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
end
end;