算額（その175） - 算額あれこれ

岐阜県不破郡垂井町宮代南宮大社奉納算額天保13年

http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF
キーワード：円複数個，楕円
#Julia #SymPy #算額 #和算 #数学

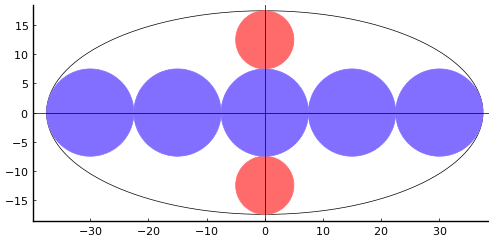
第一問　楕円内に赤円 2 個と最も多くの青等円を奇数個入れる。赤円 2 個と青円 1 個の直径の輪は短径に等しい。また，楕円の左右の端で青円は楕円に接する。赤円と青円の径を知って，青等円の個数を求めよ。

赤円，青円の半径をそれぞれ \(r_1,\ r_2\) とおく。以下の方程式を立てる。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms n::integer, r1::positive, r2::positive, x::positive, y::positive;
eq1 = x^2/(n*r2)^2 + y^2/(r2 + 2r1)^2 - 1
eq2 = (x -(n - 1)r2)^2 + y^2 - r2^2;

\(eq2 - eq1\cdot (r_2 + 2r_1)^2\) が \( (x - n r_2)\) の因子を持つので

eq3 = eq2 - eq1*(r2 + 2r1)^2 |> factor
eq3 |> println

-(-n*r2 + x)*(n^3*r2^3 - 2*n^2*r2^3 - n^2*r2^2*x + 4*n*r1^2*r2 + 4*n*r1*r2^2 + n*r2^3 + 4*r1^2*x + 4*r1*r2*x + r2^2*x)/(n^2*r2^2)

除算して簡約化する。

eq4 = eq3 / (x - n*r2) |> simplify
eq4 |> println

-n*r2 + 2*r2 + x - 4*r1^2/(n*r2) - 4*r1/n - r2/n - 4*r1^2*x/(n^2*r2^2) - 4*r1*x/(n^2*r2) - x/n^2

\(x = n r_2\) を代入して \(n\) について解くと解が得られる。

solve(eq4(x => n*r2), n)[1] |> println

(2*r1 + r2)^2/r2^2

なお，演算順序を変えると解が求まらないことがある。

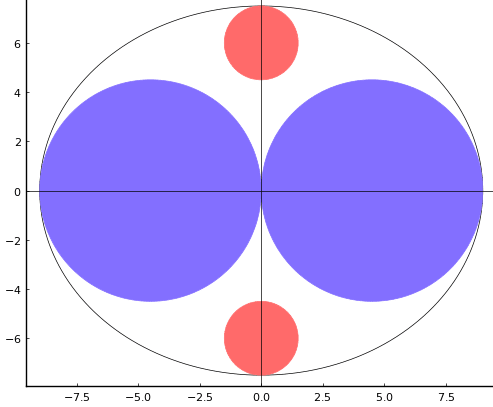
また，\(r_1,\ r_2\) にでたらめな数を与えると，題意に沿わない図になる場合がある。

\(r_1 = 3,\ r_2 = 9\) のとき，青円は偶数個になる。

描画関数プログラムのソースを見る

function draw(R1, R2, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2) = (R1, R2) ./ 2
n = floor(Int, (r2 + 2r1)^2/r2^2)
plot()
ellipse(0, 0, n*r2, r2 + 2r1)
circlef(0, r2 + r1, r1, :indianred1)
circlef(0, -r2 - r1, r1, :indianred1)
for i = -(n - 1)//2:(n - 1)//2
circlef(2i*r2, 0, r2, :slateblue1)
end
if more
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
end
end;