算額（その164） - 算額あれこれ

岐阜県大垣市西外側町大垣八幡神社（大垣八幡宮）天保年間

http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF
キーワード：円4個，二等辺三角形
#Julia #SymPy #算額 #和算 #数学

第15問: 二等辺三角形に内接する黃円を描き，その間に黒円 1 個と赤円 2 個を容れる。赤円と黒円の直径を知って黃円の直径を求めよ。

二等辺三角形の底辺の長さを \(2x\)，高さを \(y\)
黄円の半径と中心座標を \(r_1,\ (0,\ r_1)\)
黒円の半径と中心座標を \(r_2,\ (0,\ 2r_1 + r_2)\)
赤円の半径と中心座標を \(r_3,\ (x_3,\ y_3)\)
とおき，以下の連立方程式を解く。

一度に解くと有限の時間内に解が求まらないので，逐次解いていく。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms r1::positive, r2::positive, r3::positive, x3::positive, x::positive, y::positive;

eq1 = x3^2 + (r1 - r3)^2 - (r1 + r3)^2 |> simplify # 黃円と赤円が外接する
eq2 = dist2(0, y, x, 0, 0, 2r1 + r2, r2) # 円の中心から斜辺までの距離
eq3 = dist2(0, y, x, 0, 0, r1, r1) # 円の中心から
eq4 = r3*x - r1*(x - x3); # 三角形の相似

まず，eq1 を解いて \(x_3\) を求める。

ans_x3 = solve(eq1, x3)[1]
ans_x3 |> println

2*sqrt(r1)*sqrt(r3)

eq4 の \(x_3\) に \(ans_{x3}\) を代入して，\(x\) を求める。

eq4 = eq4(x3 => ans_x3)
ans_x = solve(eq4, x)[1]
ans_x |> println

2*r1^(3/2)*sqrt(r3)/(r1 - r3)

同様にして，eq3 を解き \(y\) を求める。

eq3 = eq3(x3 => ans_x3, x=> ans_x);
ans_y = solve(eq3, y)[1]
ans_y |> println

8*r1^2*r3/(4*r1*r3 - (r1 - r3)^2)

\(x_3,\ x,\ y\) を eq2 に代入して，\(r_1\) を求める。

eq2 = eq2(x3 => ans_x3, x=> ans_x, y => ans_y) |> simplify |> numerator |> (x -> x/(16r1^4*r3))
ans_r1 = solve(eq2, r1)[2]
ans_r1 |> println

2*sqrt(r2)*sqrt(r3) + r3

「黒円の半径と赤円の半径の積の平方根を取り，2 倍して赤円の半径を加える」という，「術」と同じ式が得られる。

以上をまとめると，次のようになる。

\(r_1 = 2\sqrt{r_2 r_3} + r_3\)
\(y = 8r_1^2 r3/(4r_1 r_3 - (r_1 - r_3)^2)\)
\(x = 2r_1^\frac{3}{2}\sqrt{r_3}/(r_1 - r_3)\)
\(x_3 = 2\sqrt{r_1 r_3}\)

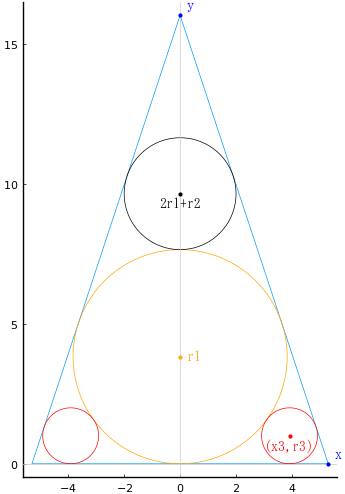
冒頭の図は，黒円と赤円の半径がそれぞれ 2，1 の場合のものである。

黒円の直径が 4，赤円の直径が 2 のとき，黄円の直径は 7.656854249492381 である。

\(r_1 = 3.8284271247461903,\ x_3 = 3.913273373914064\)
\(x = 5.296824443579761,\ y = 16.0321995349166\)

描画関数プログラムのソースを見る

function draw(r2, r3, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = 2sqrt(r2*r3) + r3
y = 8r1^2*r3/(4r1*r3 - (r1 - r3)^2)
x = 2r1^(3/2)*sqrt(r3)/(r1 - r3)
x3 = 2sqrt(r1*r3)
@printf("黒円の直径が %g，赤円の直径が %g のとき，黄円の直径は %g である。\n", 2r2, 2r3, 2r1)
@printf("r1 = %g; r2 = %g; r3 = %g; x3 = %g; x = %g; y = %g\n", r1, r2, r3, x3, x, y)
plot([x, 0, -x, x], [0, y, 0, 0], color=1, lw=0.5)
circle(0, r1, r1, :orange)
circle(0, 2r1 + r2, r2, :black)
circle2(x3, r3, r3)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, r1, " r1", :orange, :left, :vcenter)
point(0, 2r1 + r2, "2r1+r2", :black, :center, delta=-delta/2)
point(x3, r3, "(x3,r3)", :red, :center, delta=-delta/2)
point(x, 0, " x", :blue, :left, :bottom, delta=delta/2)
point(0, y, " y", :blue, :left, :bottom, delta=delta/2)
end
end;