算額（その72） - 算額あれこれ

埼玉県浦和市西堀氷川神社嘉永5年(1852)

埼玉県立図書館：埼玉県史料集第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

和算の館
http://www.wasan.jp/saitama/uhikawa.html

キーワード：円3個，正方形
#Julia #SymPy #算額 #和算 #数学

正方形の中に大円，中円，小円が互いに接して入っている。中円の直径が 10 寸のとき，小円の直径はいかほどか。

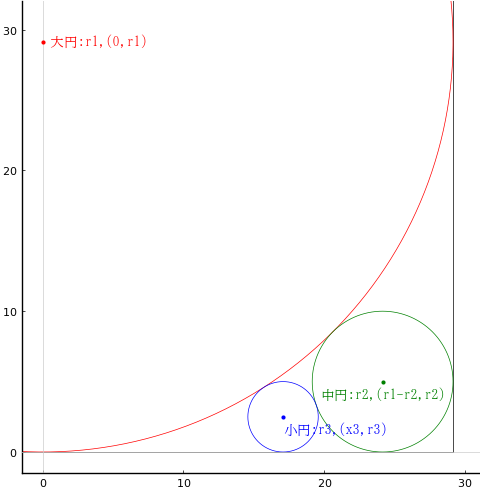
大円の半径と中心座標を \(r_1,\ (0,\ r_1)\)
中円の半径と中心座標を \(r_2,\ (r_1 - r_2,\ r_2)\)
小円の半径と中心座標を \(r_3,\ (x_3,\ r_3)\)
とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms r1::positive, r2::positive, x3::positive, r3::positive
eq1 = (r1 - r2)^2 + (r1 - r2)^2 - (r1 + r2)^2;
eq2 = x3^2 + (r1 - r3)^2 - (r1 + r3)^2;
eq3 = (r1 - r2 - x3)^2 + (r2 - r3)^2 - (r2 + r3)^2;
res = solve([eq1, eq2, eq3], (r1, r3, x3))[2] # 2 of 3

(r2*(2*sqrt(2) + 3), r2/2, r2*(sqrt(2) + 2))

# r3: 小円の半径
res[2]

\(\displaystyle \frac{r_{2}}{2}\)

小円の半径 \(r_3\) は中円の半径 \(r_2\) の 1/2 である。
中円の直径が 10 寸ならば、小円の直径は 5 寸である。

描画関数プログラムのソースを見る

function draw(r2, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="")#, fontfamily="IPAMincho")
(r1, r3, x3) = (r2*(2*sqrt(2) + 3), r2/2, r2*(sqrt(2) + 2))
plot([-r1, r1, r1, -r1, -r1], [0, 0, 2r1, 2r1, 0], color=:black, lw=0.5)
circle(0, r1, r1)
circle(r1 - r2, r2, r2, :green)
circle(x3, r3, r3, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, r1, " 大円:r1,(0,r1)", :red, :left, :vcenter)
point(r1 - r2, r2, "中円:r2,(r1-r2,r2)", :green, :center, delta=-delta/2)
point(x3, r3, "小円:r3,(x3,r3)", :blue, :left, delta=-delta/2)
plot!(xlims=(-0.05r1, 1.1r1), ylims=(-0.05r1, 1.1r1))
end
end;