大阪府茨木市 井於神社 弘化3年(1846)
和算の館
http://www.wasan.jp/osaka/iyo.html
キーワード:円,面積
#Julia #SymPy #算額 #和算 #数学
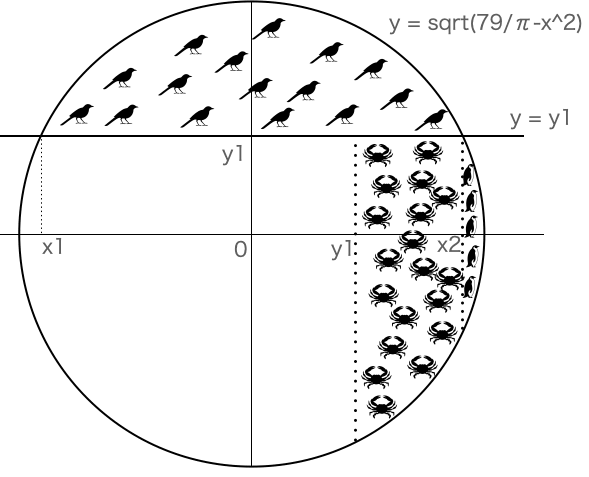
面積が 79 の円の半分を欠き取る \(x = y_1 - x_1\) の長さを求めよ。

include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms y()::positive;
@syms x::real, x1::negative, x2::positive, y1::positive, r::positive;
面積が 79 ということは,半径 \(r\) とすると \(\pi r^2 = 79\) ゆえ
r = solve(PI * r^2 -79, r)[1]
r |> println
sqrt(79)/sqrt(pi)
円の中心を原点とし,円の上半分の方程式は
y = sqrt(79/PI - x^2)
y |> println
sqrt(-x^2 + 79/pi)
\(y = y_1\) との交点の \(x\) 座標を \(x_1,\ x_2\) と置く。
x1, x2 = solve(y - y1, x)
x1 |> println
x2 |> println
-sqrt(-pi*y1^2 + 79)/sqrt(pi)
sqrt(-pi*y1^2 + 79)/sqrt(pi)
添付図で「鳥」がいる部分の面積
s1 = integrate(y-y1, (x, x1, x2))
s1 |> println
-y1*sqrt(-pi*y1^2 + 79)/sqrt(pi) + 79*asin(sqrt(79)*sqrt(-pi*y1^2 + 79)/79)/pi
添付図の「カニ」のいる部分の面積は
s2 = integrate(y1+y, (x, y1, x2));
s2 |> println
-y1^2 + y1*sqrt(-pi*y1^2 + 79)/sqrt(pi) + 79*asin(sqrt(79)*sqrt(-pi*y1^2 + 79)/79)/(2*pi) - 79*asin(sqrt(79)*sqrt(pi)*y1/79)/(2*pi)
添付図の「ペンギン」のいる部分の面積は
s3 = 2integrate(y, (x, x2, sqrt(79/PI)));
s3 |> println
-y1*sqrt(-pi*y1^2 + 79)/sqrt(pi) - 79*asin(sqrt(79)*sqrt(-pi*y1^2 + 79)/79)/pi + 79/2
eq1 = s1+s2+s3 - 79//2;
simplify(eq1)|>println
-y1^2 - y1*sqrt(-pi*y1^2 + 79)/sqrt(pi) + 79*asin(sqrt(79)*sqrt(-pi*y1^2 + 79)/79)/(2*pi) - 79*asin(sqrt(79)*sqrt(pi)*y1/79)/(2*pi)
solve(eq1) では解けない。
# solve(eq1, y1)
図を描いてみる。横軸は \(y_1\) で,変域は \(\left [0, \sqrt{79/\pi} \right ]\)
using Plots
plot(s1, label="s1", xlims=(0, 5), aspectratio=:none)
plot!(s2, label="s2")
plot!(s3, label="s3")
plot!(s1+s2+s3, label="s1+s2+s3")
hline!([79/2], label="79/2")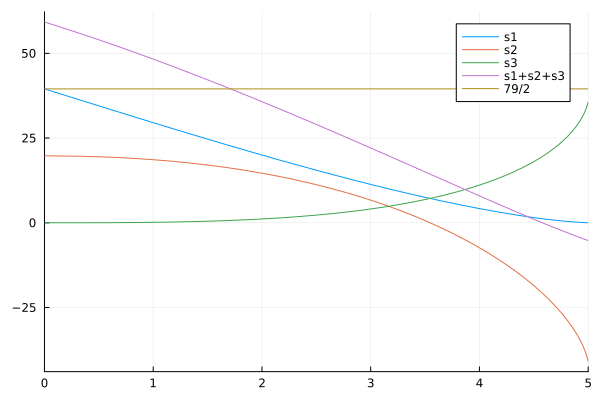
eq1 を図示する。
using Plots
func(y1) = -y1^2 - y1*sqrt(-pi*y1^2 + 79)/sqrt(pi) + 79*asin(sqrt(79)*sqrt(-pi*y1^2 + 79)/79)/(2*pi) - 79*asin(sqrt(79)*sqrt(pi)*y1/79)/(2*pi)
plot(func, aspectratio=:none, xlims=(0, 5))
vline!([1.711])
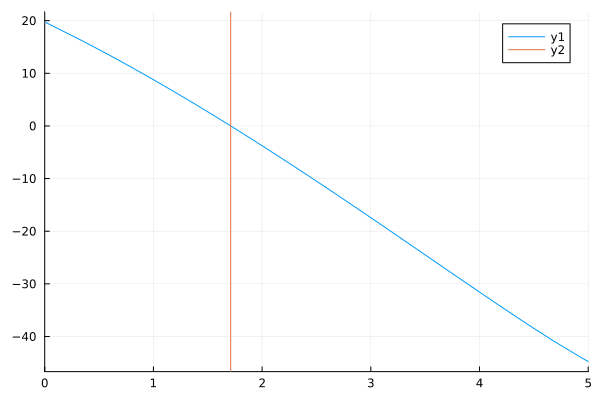
\(\text{func}(y_1) = 0\) となる \(y_1\) を,find_roots() で解く。
using Roots
find_zero(func, (0, 4))
1.7111132936192583
\(y_1 = 1.7111132936192583\) のときに \(\text{func}(y_1) = 0\) である。
算額に言う「一辺の長さ」は \(\text{abs}(x_1) + y_1\)
abs(x1(y1=> 1.7111132936192583)) + 1.7111132936192583 |> N
6.424771353440623
6.42477... となったが,算額では 6寸3分8厘7毛すなわち 6.387 といっている。
検算してみよう。
(s1 + s2 + s3)(y1 => 1.7111132936192583) |> N
39.5
SymPy で得られた答えが正しいようだ。
以下のアイコンをクリックして応援してください