CodeIQで「『データサイエンティスト養成読本』著者陣さんの問題」やってみたけど…
http://m884.hateblo.jp/entry/2013/09/19/171218
なんですけどね。どっちもどっち???
問題文は孫引き(大元の記事は参照できなくなっている)だが,
問1. Rに標準装備されているあやめ(Iris)のデータを用いて、あやめのがく片の長さ(Sepal.Length)とがく片の幅(Sepal.Width)の相関分析を行いました。
【Rの実行結果】
上記の【Rの実行結果】を参考にし、次の中から正しいものを一つ選んでください。
a) LengthとWidthの間の相関係数r=-0.11757となっているため、Lengthが大きいほど、Widthが小さくなるといえる
b) 相関係数rの検定結果でp値が0.1519と有意水準0.05(5%)より大きくなっているため、2変数間に有意な相関があるとはいえない
c) aとbで統計量を精査しているため、データをプロットして散布図を作成することに意味はない
R の実行結果は示されていないが,
> cor.test(iris$Sepal.Length, iris$Sepal.Width)
Pearson's product-moment correlation
data: iris$Sepal.Length and iris$Sepal.Width
t = -1.4403, df = 148, p-value = 0.1519
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.27269325 0.04351158
sample estimates:
cor
-0.1175698
でもあろうか。
ブログ筆者:正解はbらしいのですが、私はaと答えました。なんでaじゃないのかちょっとよくわかりません。なんか根本的に勘違いしているんでしょうか…。
出題者のレビュー:aは、相関係数の理解が誤っています。
相関係数は-1から1の値をとり、その符号で相関関係の方向性を表し、絶対値の大きさで相関関係の強さを示します。
一般的には次のように言われることが多いです。
|r|=0.7~1:強い相関あり
|r|=0.4~0.7:やや相関あり
|r|=0~0.2:ほとんど相関なし
b については,
ブログ筆者:bが正解となっていますが、微妙なラインですが私は誤りだと思います。「有意水準0.05(5%)より大きくなっているため」というのは有意水準を所与のものとしている書き方だと思います。「有意水準を5%に定めた場合は」とすべきでしょう。
=======================
c での散布図に関しての書きぶりからは,「R の実行結果」に散布図は示されていないのではないかと思った次第だが,散布図は以下のようになる。
plot(iris$Sepal.Length, iris$Sepal.Width, cex=0.5)
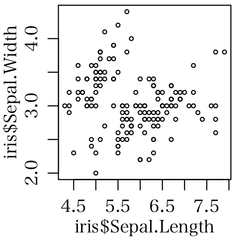
残念ながら,このような単純な散布図では,「負の相関で相関係数は -0.11757」ということしか分からないだろう。
しかし,iris データについては,iris$Species を適切に評価しないと正しい分析は出来ないことはよく知られていると思うのだが。知らなくても,注意深い人は左上に位置するデータの様相が気になるかもしれない。
iris$Species を考慮した,以下のような「適切な散布図」を描けば,iris データの真相に迫れるだろう。
plot(iris$Sepal.Length, iris$Sepal.Width, cex=0.5,
col=rep(c("#aa000060", "#00aa0060", "#0000aa60"), each=50),
pch=rep(c(15, 16, 17), each=50))

つまり,Sepal.Length と Sepal.Width の関連の程度は Species により若干は異なるものの,二変数には正の相関があるということである。
> lapply(split(iris, iris$Species), function(d) cor.test(d$Sepal.Length, d$Sepal.Width))
$setosa
Pearson's product-moment correlation
data: d$Sepal.Length and d$Sepal.Width
t = 7.6807, df = 48, p-value = 6.71e-10
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.5851391 0.8460314
sample estimates:
cor
0.7425467
$versicolor
Pearson's product-moment correlation
data: d$Sepal.Length and d$Sepal.Width
t = 4.2839, df = 48, p-value = 8.772e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.2900175 0.7015599
sample estimates:
cor
0.5259107
$virginica
Pearson's product-moment correlation
data: d$Sepal.Length and d$Sepal.Width
t = 3.5619, df = 48, p-value = 0.0008435
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.2049657 0.6525292
sample estimates:
cor
0.4572278
解答の選択肢 a も b も,Species の存在を考慮していない。適切な分析をすれば,正反対の結果になる。Species ごとに分析すれば,Sepal.Width と Sepal.Length 間には有意な正の相関が認められる。
ちなみに,選択肢 c は誤りであるのは明白だが,不適切な散布図では描いても意味がない。
結論として,問 1 には正解がない。